Применение спектрального анализа биржевой информации или Эффект Бабочки. Часть 1.

К активному обсуждению предлагаются несколько переводов, перепостов, а также собственных идей:

Базовая идея анализа временного ряда по Фурье состоит в том, чтобы разделить данные на сумму синусоид с различными длинами циклов, где каждый цикл является частью длины общего или фундаментальной цикла. Например, Рисунок 1 показывает временные ряды, состоящие из линейного тренда и двух главных циклов, а Рисунок 2 дает разложение на составляющие синусоиды.

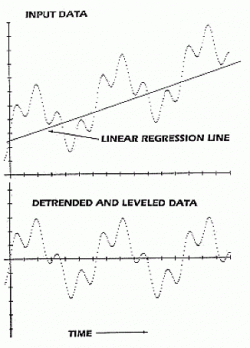
Рисунок 1


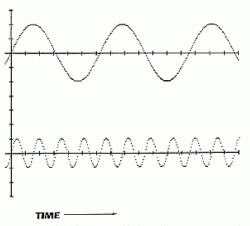
Рисунок 2

Первоначально циклический анализ применялся к физическим явлениям, чтобы описать поведение сложных колебаний, к примеру, множественные колебания, созданные струнным инструментом. Анализ таких систем изящно описан поведением самого длинного или фундаментального цикла, и ответом на первую, вторую и более высокого порядка гармоники фундаментального. Позже Фурье и другие расширили этот анализ и показали, что любой конечный сегмент или кривая данных могут быть хорошо приближены рядом синусоид. Этот метод — основа анализа Фурье данных (временные ряды) и обычного анализа спектра. Примечание: приближение Фурье кривой или временных рядов будет периодическим, даже если данные не являются таковыми!

Чтобы понять спектральный анализ Фурье, кратко рассмотрим свойства отдельной синусоиды. Синусоида может уникально быть охарактеризована в любой точке времени своей амплитудой или максимальной величиной, своей частотой или нормой вибрации и своей фазой. (См. Рисунок 3.)


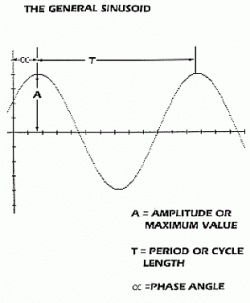
Рисунок 3

Период или длина цикла синусоиды — число торговых дней в году (предположим, что один год — 260 торговых дней) деленный на частоту, то есть синусоида с частотой 10 циклов в год имеет период 260 / 10 = 26 дней. Анализ Фурье разделяет данные на сумму синусоид соответствующей амплитуды, частоты и фазы. Спектральный анализ Фурье — конденсат этих преобразованных данных, посредством чего квадрат амплитуды или сила каждой синусоиды выражается против частоты каждой синусоиды. (Информация о фазе, таким образом, в представлении спектра данных теряется.) Например, спектр амплитуды циклических данных на Рисунк 1 состоит из двух пиков данных на соответствующих частотах, как показано на Рисунке 4.


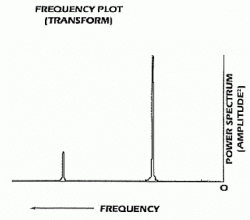
Рисунок 4.


Основное отличие между анализом Фурье непрерывных кривых и данных типа закрытий акций или товаров в том, что для данных существует верхний предел частотного спектра. Для дневных данных частоты выше, чем 130 (двухдневный цикл) неотличимы от частот, меньших 130. Это следствие осуществления процесса выборки, подобно стробоскопу в оптике. Таким образом, анализ Фурье данных уместен только в частотах между 0 и 130 циклов в год.
Спектральный анализ полезен для технического анализа, где он обеспечивает количественный инструмент для обнаружения доминирующих частот или полос частот в данных пользователя. В частности, мы можем использовать спектральный анализ, чтобы помочь выбрать средние для различных видов технического анализа. Средние (и другие методы фильтрования данных) позволяют нам подчеркнуть только те частоты или спектральные полосы, которые интересны для целей торговли. Вообще, мы можем разделить спектр дневных торговых данных на три родовые спектральные полосы:
· НИЗКОЧАСТОТНЫЕ КОМПОНЕНТЫ — представлены сезонными трендами и долгосрочными моделями. Обычно сюда включаются частоты в диапазоне от 0 до 4, то есть циклы, большие 60 дней.
· ПРОМЕЖУТОЧНЫЕ ЧАСТОТЫ — представлены краткосрочные торговые циклами и рыночные циклы хода/коррекции. Обычные частоты находятся в диапазоне от 4 до 40, соответствуя периодам между 6 и 60 днями.
· ВЫСОКОЧАСТОТНЫЕ КОМПОНЕНТЫ — случайные дневные изменения или торговый «шум». Как правило, большая часть спектра находится в этой полосе, то есть, частотах от 40 до 130 — циклах меньших, чем 6 дней.



Рисунок 5 демонстрирует спектр Фурье и дневные цены на протяжении 110 дней (24 недели) полученных по закрытиям соевого масла, используя основной спектральный код, данный в конце этой статьи. (Примечание: нулевая частота — справа.) В данном случае есть две области спектра, представляющие интерес: полоса промежуточных частот, которая достигает максимума приблизительно на 16 циклах в год (период 16 дней) и спектральный пик на 32 циклах в год (период 8 дней). Остальная часть спектра содержит главным образом шумовые колебания, в нем нет больше низких частот, так как до вычисления спектра из данных был убран тренд. (Пик на 6 циклах в год (период 43 дня) представляет собой низкочастотную составляющую.)



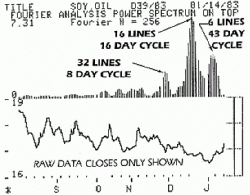
Рисунок 5.


Все это, однако, еще цветочки в использовании этого метода анализа,. Есть две основных проблемы, которые могут исказить или дискредитировать результаты: непостоянство данных и чрезмерный шум. Непостоянства данных приводят к большим колебаниям спектра, которые затеняют основные циклические компоненты, а шум может давать ложные пики и впадины спектра. Кроме того, если точки начала и конца данных неодинаковы, анализ Фурье может быть искажен. (Причина в том, что анализ Фурье пытается приближать периодическое расширение данных. Когда конечные точки не равны, создается неоднородность в периодически продлеваемых данных.) Следовательно, большинству программ спектрального анализа свойственны эти проблемы. Поэтому для анализа рекомендуются длинные интервалы данных, содержащие по крайней мере 64 дневных наблюдения для сглаживания шума и для решения спектральных пиков.
Коды спектра Фурье разработаны для использования в системе CompuTrac, но могут быть приспособлены и к другим компьютерным системам. Сердце этого кода — процедура быстрого преобразования Фурье (Fast Fourier Transform), которая достаточно быстро вычисляет разложение Фурье для использования на ряде данных умеренной длины, то есть, до 512 точек данных.
Мы можем использовать упомянутый выше код, чтобы найти пиковые частоты спектра и подобрать фильтры для данных, например скользящие средние с параметрами, оптимизированными к данным и частотным полосам. Число точек в расширенном массиве дается в заглавной информации (N=xxx), а основная частота или частотная дельта между спектральными линиями составляет всего лишь 260N, т.е. 260/256 для спектра соевого масла, показанного на рисунке 5. Чтобы найти пиковую частоту спектра, лишь пересчитывают число спектральных линий от нулевой частоты до спектрального пика, и умножают его на частотную дельту 260/N. Например, первый спектральный пик от нижней полосы частот на рисунке 5 отстоит на 16 линий от нулевой частоты, поэтому пик частоты находится на 16*260/256 = 16.25 (длина цикла = N/номер линии = 256/16 = 16 дней.)
Одно из практических применений для анализа спектра — выявить подходящие периоды средних для сокращения влияния нежелательных частот. Средняя с длиной M дней сведет на нет или сократит амплитуду любой синусоиды с длиной цикла, меньшей M, т.е. частоты, большие, чем 260/M, при сохранении амплитуды синусоид с длинами цикла большими, чем 1.5*M. Поэтому долгосрочный трейдер может использовать анализ спектра, чтобы подобрать такой период средней, который сохранит всю силу низких частот необработанных данных, но значительно снизит влияние любых промежуточных или высокочастотных спектральных пиков. (Период скользящей средней можно проверить, сравнивая спектр необработанных данных со спектром усредненных данных.) Трейдер, работающий в промежуточном сроке, может использовать спектральный анализ, чтобы найти акции или товары с сильными пиками промежуточных частот, и подобрать периоды средних, которые отфильтруют как высоко-, так и низкочастотные спектральные влияния. (Это основная идея в осцилляторном анализе.)



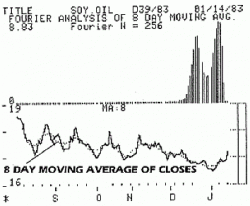
Рисунок 6.


Например, мы можем исключить влияние частот выше 16 циклов/в год (период 16 дней), применяя 8-дневную среднюю к данным соевого масла (рисунок 5). Спектр Фурье для данных, усредненных 8-дневной средней, показанный на рисунке 6, подтверждает, что после сглаживания в данных остаются только первые два спектральных пика.


Автор: Anthony Warren