Обобщенная модель ценообразования опционов
Я попробую небольшими частями изложить основные положения обобщенной теории опционов. При ее разработке не использовалась гипотеза о случайном поведении цены базового актива по причине того, что для большинства финансовых рынков ее невозможно ни подтвердить, ни опровергнуть. Обобщенная теория индифферентна по отношению к причинам ценовых изменений и в этом ее отличие от классической теории опционов, для которой гипотеза о случайном поведении цен является незыблемым основанием. Важно отметить, что в случае согласия с гипотезой классическая теория не вступает в противоречие с обобщенной, но оказывается ее составной частью. Отсюда и название “обобщенная”. Она должна понравиться тем, кто не очень хорошо разбирается в методах ТВ и МС, но хочет разобраться в опционах.
Постараюсь обойтись минимальным количеством формул, хотя совсем без математики не получится. Поэтому, если что-то будет непонятно, спрашивайте.
Размещать новые части я буду с частотой примерно раз в неделю, по мере их написания. Всего частей будет, наверное, четыре или пять.
Некоторые куски текста выделены курсивом. Это Замечания, которые читать не обязательно.
Первое Замечание. Под гипотезой о случайном поведении цен я понимаю любую из набора гипотез, предполагающих, что поведение цены базового актива подчинено модели случайности. Таких моделей много – броуновское движение, геометрическое броуновское движение, винеровский процесс и т.д. Ни одна из них нам не понадобится. Все, что нужно знать о поведении цены базового актива – это то, что она меняется.
Обобщенная теория опционов
Часть 1. Что не так с классической теорией
Открываем Википедию на страничке Модель Блэка — Шоулза и читаем первое из допущений модели:
“Торговля базовым активом ведется непрерывно, и поведение его цены подчиняется модели геометрического броуновского движения с известными параметрами ”.
Попробуем представить себе рынок, на котором поведение цены БА подчиняется закону геометрического броуновского движения (GBM). Он должен состоять из очень большого числа одинаково мелких игроков, каждый из которых в произвольные моменты времени и независимо от других игроков принимает решение о покупке или продаже БА на основании результатов подбрасывания монеты. Если рынки устроены именно так, то для изучения опционов достаточно ограничиться классической теорией. Если же хотя бы одно из условий вызывает сомнение, то есть повод засомневаться и в самой теории.
Главный вопрос даже не в том, вправе ли мы рассматривать процесс ценообразования БА как GBM, а в том, можно ли вообще считать этот процесс случайным.
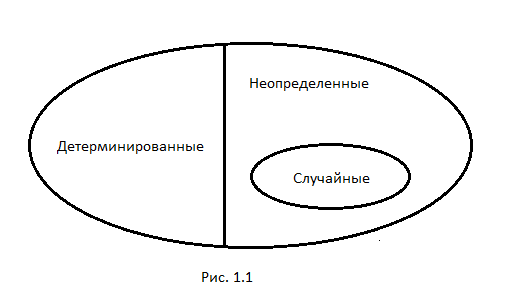
Назовем неопределенным явление, исход которого, в отличие от детерминированного, невозможно точно предсказать заранее.
Среди неопределенных есть очень специальный класс явлений, которые называются случайными. Для них можно, во-первых, полностью описать множество возможных исходов, и во-вторых, должен существовать способ, с помощью которого каждому из исходов ставится в соответствие детерминированное число – вероятность, служащая объективной мерой возможности его наступления.
Если эти условия не выполнены, а множество исходов или их вероятности берутся “с потолка”, то аппарат ТВ и МС принесет больше вреда, чем пользы.
Методов нахождения исходных (элементарных) вероятностей, по сути, только два. Первый предполагает, что объекты специально сконструированы так, чтобы наделить их заданными вероятностными свойствами. Это игральные кости, карты, рулетка.
Теоретически, финансовый рынок тоже можно сконструировать. Если в какой-нибудь удивительной стране игрокам на законодательном уровне будет предписано покупать и продавать активы только на основании результатов подбрасывания монеты, то можно будет утверждать, что поведение цен в этой стране подчинено законам GBM.
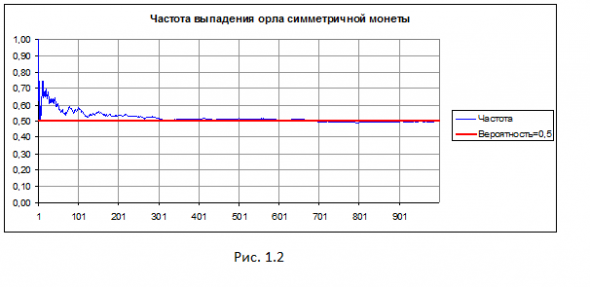
Теперь обсудим распространенное мнение о преимуществе математиков над гуманитариями в играх, основанных на неопределенности. Рассмотрим симметричную монету. Априори (до опыта) известно, что вероятность выпадения орла равна 0,5. На основании этого математик может вычислить вероятность любого сложного события, например, вероятность выпадения трех орлов подряд в серии из десяти испытаний. Это, действительно, даст ему преимущество над гуманитарием, который, не зная правил комбинаторики, возьмет вероятность сложного события “с потолка”.
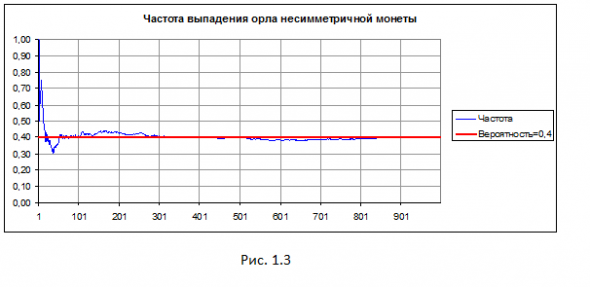
Изменим условия, пусть теперь монета изогнута. Вероятность выпадения орла априори не известна, на помощь приходит второй метод — статистических испытаний. Согласно Закону Больших Чисел в бесконечной серии испытаний при неизменных условиях частота события стремится к его вероятности. Оценив эту вероятность с любой наперед заданной точностью, математик сохранит преимущество над гуманитарием.
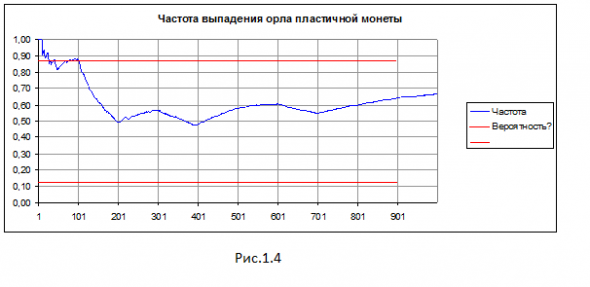
Изменим условия еще раз. Предположим, что металл, из которого изготовлена монета, настолько пластичен, что монета меняет свою форму после каждого броска. Условия Закона Больших Чисел нарушены. При каждом испытании мы, по сути, имеем дело с другой монетой, частота никуда не сойдется. Математик будет вынужден взять неизвестную ему исходную вероятность “с потолка” и найденная на ее основе вероятность сложного события окажется не точнее той, что возьмет “с потолка” гуманитарий. Математик теряет свое преимущество.
Симметричная монета. Эксперимент можно не проводить. Частота сойдется к 0,5 априори
Несимметричная монета. Эксперимент достаточно провести один раз. В любом следующем эксперименте частота сойдется к тому же пределу
Пластичная монета. Частота никуда не сходится (сойдется к 0 или 1, если монета свернется в трубочку, но это вырожденный случай). Хорошая тема для дискуссии — можно ли использовать термин “вероятность” применительно к тому, что нельзя измерить.
Эти же рассуждения можно отнести и к финансовым рынкам. В большинстве своем они нестационарны (пластичны), это значит, что правомерность использования методов ТВ и МС в каждом конкретном случае нужно оговаривать отдельно. Если этого не делать, то любые статистические оценки окажутся цифрами “с потолка”, как и результаты всех дальнейших расчетов. Поэтому перед тем, как решать задачу из серии: “Доходности акций компании A и их вероятности представлены в таблице …” спросите автора задачи, откуда он эти вероятности взял.
В следующей главе мы рассмотрим понятие подвижности (mobility) – числовой характеристики активности рынка, которая, в отличие от волатильности, не предполагает того, что цены изменяются в соответствии со случайными законами.














С возвращением! Скучал без Ваших оригинальных идей.
Сейчас с куклом на страйке 64 500 разберусь — и сразу сяду вникать.
Формул можно и побольше. Зачастую это в 100 раз понятней и проще, чем исписать десятки килобайт размахивания руками.
С уважением