Сишный АнтиБаффет, с днем рождения! АКФ тебе в качестве подарка.
Всем привет!
Ну что же, вчера был день рождения у бота, за которым я уже год как пристально слежу...
Интересно наблюдать как он растет, набирается сил, падает, а затем снова растет...
3 года это уже не хухры-мухры!
Вот здесь мы с ребятами обсуждали тему АКФ и поняли, что пока на практике ее «не пощупаем», то и не поймем для чего она нужна и нужна ли вообще?
Итак, что же дано?
Дано:
1. Теоретические азы мы черпаем здесь
2. Ну и в качестве испытуемого берем Сишного АнтиБаффета
Поехали!
Эквити за 3 года:
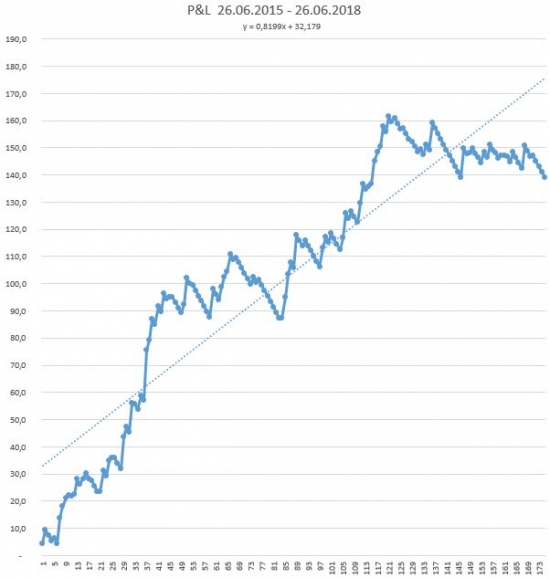
В качестве случайного процесса у нас будут выступать дневные приращения Эквити в % (без реинвестирования):
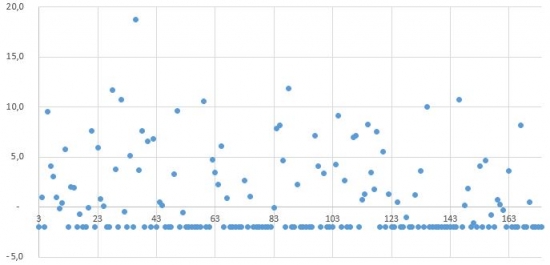
Далее мы считаем автокорреляционную функцию временного ряда, для этого мы выстраиваем вот такую вот матрицу дневных приращений:
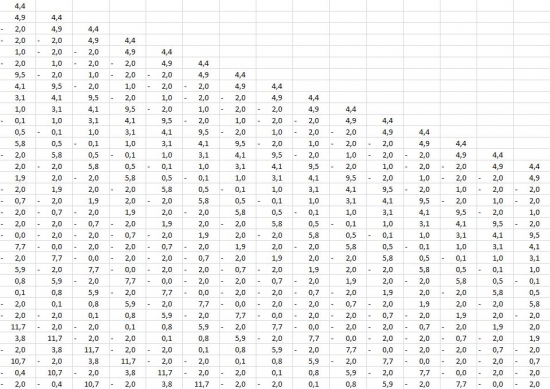
Коэффициенты автокорреляции первого, второго уровня и т.д. считаются очень просто в экселе, достаточно выделить два ряда и воспользоваться встроенный функцией "=коррел(...)".
Вот так это выглядит для вычисления коэффициента корреляции 5-го порядка:
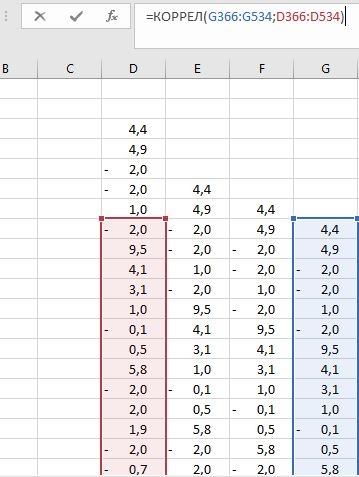
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.
Вот наша коррелограмма вплоть до 30-го лага:
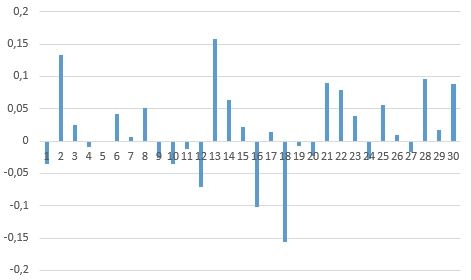
Теперь снова возвращаемся к теории и вспоминаем следующее:
При помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Анализ структуры ряда можно проводить следующим образом:
- если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию;
- если наиболее высоким оказался коэффициент автокорреляции порядка "τ", ряд содержит циклические колебания с периодичностью в "τ" моментов времени;
- если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из предположений относительно структуры ряда:
- ряд не содержит тенденции и циклических колебаний, а включает только случайную компоненту,
- ряд содержит сильную нелинейную тенденцию.
Выводы:
Мы видим, что наиболее значимыми коэффициентами автокорреляции являются коэффициент 13-го (0,158) и 18-го порядка (-0,157), т.е. делаем вывод, что наш ряд содержит циклические колебания с периодичностью в 13-ть и 18-ть периодов времени.
Эту же цикличность также можно наблюдать графически, особенно если посмотреть на просадки (это интереснее всего):
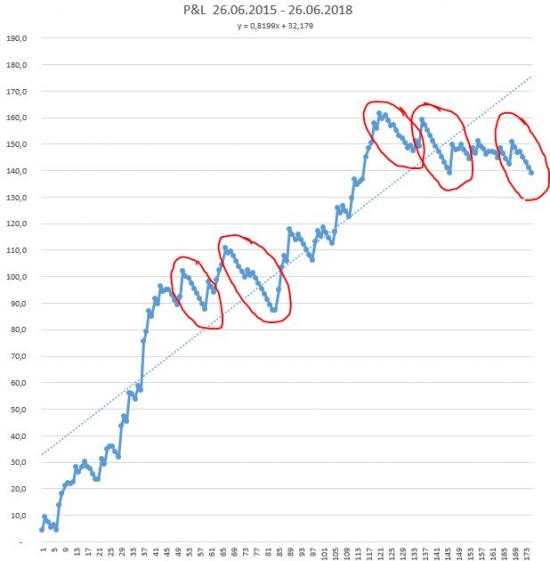
Главный вывод: АКФ полезна для определения периодичности циклических колебаний. Фондовый рынок — это временная структура, все здесь повторяется и любая стратегия будет обладать некой цикличностью временной структуры!
Oleg Only Algo , дружище, спешл фо ю!
А. Г. , как вы считаете, если коэффициент автокорреляции не важно какого порядка меньше 0,5, стоит ли вообще на это обращать внимание?
Когда мы ищем корреляцию ряда самим с собой (автокорреляцию), то ковариация (х, х) =0 и сигмы равны нулю в случае прямой эквити.
Итого будет 0/0. Математически я не помню как доказать, что автокорреляция ряда с самим собой равна 1, но по смыслу это так, т.к. ряды полностью идентичны.
в моем случае будет правильный вывод:
ряд не содержит тенденции и циклических колебаний, а включает только случайную компоненту.
А для примера «фиг вам» похоже правильный вывод:
если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию;
Видимо, эта периодичность тоже тенденцией считается, только периодической.
Было бы интересно подобрать пример, где коэффициент корреляции для первого лага был бы больше 0,5 и при этом все остальные коэффициенты для лагов были заметно ниже первого и посмотреть на эту тенденцию.
Будет время, нужно как-нибудь поиграться.
Еще одна стратегия, тот же Сишний АнтиБаффет, только от продажи:
Смысл АКФ — понять есть ли некая тенденция в нашем ряде.
В мое примере Сишного Антибаффета с коэффициентами максимальными [-0,15;0,15] никакой тенденции нет:
ряд не содержит тенденции и циклических колебаний, а включает только случайную компоненту.
Я ошибся первоначально с выводами.
Скриган строит гребенку полосовых фильтров. Пока я пользы в таких методах не нашел. Потому что (а) процесс нестационарный (б) сигнал/помеха низкие.
И хотя я уверен, что в рынке есть и недельная и месячная цикличность, то, что Вы её не обнаруживаете говорит о негодности инструмента.
1. Когда мы строим АКФ или Фурье-спектр (что одно и то же по сути) для модельных примеров типа прямоугольных импульсов, пил, синусоид, экспонент, мы обнаруживаем не то, чтобы артефакты, но то, что заранее предопределено. Что тут важно? В каждом из модельных примеров мы пониманием, что мы его строим как циклически продолжающийся бесконечно хоть влево хоть вправо и начиная с некого окна он неизбежно выглядит как стационарный и всё гуд.
2. Когда мы берем эквити от нестационарного процесса, которая сама с высокой вероятностью нестационарна, мы не знаем, какой она будет в будущем. Что важно в этом случае?
2.1. Мы анализируем растущие эквити (в кумулятивном виде).
2.2. Мы анализируем их как такие, которые буду расти дальше вправо и хорошо бы, чтобы они росли и в прошлом влево.
2.3. Мы предполагаем, что характер роста будет примерно таким же. В противном случае наши попытки анализировать цикличности бессмысленны априори.
3. А теперь представим, что у нас получается с учетом выполнения этих предположений 2.1.-2.3. Если и дальше эквити будет расти с периодическими просадками, т.е. у эквити процесса всё-таки есть удовлетворительное положительное матожидание, то уместно без анализа цикличности эквити (неважно, какими методами) после положительных серий сделок сокращать экспозицию, а после отрицательных — наращивать.
4. Т.е. желание контртрендить растущую эквити вполне обосновано чисто общим рассуждением и принятием гипотез, которые мы и так принимаем, если вкладываемся в данную стратегию. БЕЗ РАСЧЕТОВ АКФ.
5. Дальше дело техники. Любую ли эквити можно и стоит ли контртрендить и как это делать. Где-то овчинка стоит выделки, где-то — нет.
6. Но самое важное. Для принятия решения об улучшении эквити нужно опираться на кое-что иное, нежели на анализ типа АКФ.
Вывод: у нестационарных процессов мы не знаем абсолютно ничего, даже построив какую-то гипотезу на будущее постоянно попадаем в просак. :)
1. отличить закурфиченные системы от жизнеспособных, при одинаковом коде и разных, но предопределённых параметрах
2. найти факторы, которые позволяют давать перспективным сделкам больше денег
а какая там периодичность, можно без всяких сложностей посчитать (макс число убытков/прибылей подряд, макс длина просадки)
слышал мнение, что профиль сделок (% плюсов и минусов) у трейдеров может мало отличаться, при этом за счёт бюджета сделки (п 2.) опытные трейдеры получают от плюсовых сделок больше. В реальности, т.е. моих опытах, ошибки, когда хорошему плюсу даётся ошибочно мало денег, сильно убивают эквити.
Вот для чего по сути нужен этот АКФ.