Дельта-нейтральность через матожидание

Возникла тут одна идея — как можно было бы добиваться дельта-нейтральности опционной позиции. Хотел бы поделиться, может, получится интересное обсуждение. Но сначала — предыстория вопроса.

Итак, допустим, мы торгуем какую-то дельта-нейтральную стратегию. Это может быть и покупка-продажа волатильности, и котирование ММ, и календарный арбитраж между разными сериями или еще какая. Главное, после открытия опционной позиции (по выгодным, как нам кажется, ценам), нужно добавить фьючерсов в позу (лонг или шорт), чтобы минимально зависеть от того, куда пойдет базовый актив (БА). Как это сделать? Самое простое — посчитать дельту по Блеку-Шоулзу (БШ) и выровнять эту дельту соответствующим количеством фьючерсов. Рассмотрим на примере покупки волатильности:


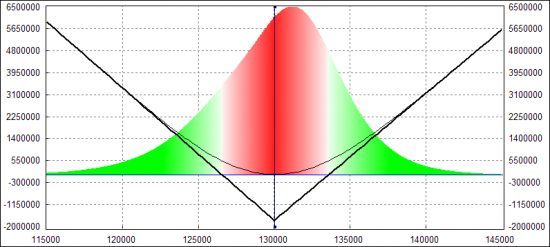
Здесь дельта БШ равна нулю и, по идее, нам все равно, куда пойдет БА. Правда будет сильная зависимость от веги, но этот риск здесь рассматривать не будем, только риск от движения БА. Судя по картинке и по тому, что дельта БШ = 0 — у нас нет такого риска. Но если мы в реале откроем эту позу, то обнаружим, что есть почти 100% корреляция эквити с БА. Если она положительная (растет БА — растет PnL, падает БА — падает PnL), то, значит, у позы фактически положительная дельта. Если корреляция отрицательная (растет БА — падает PnL, и наоборот), то фактически у нас отрицательная дельта. Несмотря на то, что БШ показывает нам нулевую дельту. Перефразируя известное выражение, можно было бы сказать так:

Если БШ показывает нулевую дельту у позиции — не верь глазам своим!

Почему же БШ ошибается? Дело в том, что у них предполагается постоянство улыбки IV при изменении цены БА. Но это очевидно неверное предположение. Улыбка будет изменяться и еще как!

Как же нам тогда поступить? Можно было бы замерить на небольшом промежутке времени, насколько изменились БА и PnL позы. И отсюда вычислить реальную дельту. Например, БА вырос на 100п, а PnL упал на 1000п. Значит, реальная дельта = -10 и мы можем внести соответствующую коррекцию в робот ДХ, чтобы он поддерживал дельту БШ равной +10, а не нулю. Дешево и сердито. Но такой метод подойдет, только если опционная поза не меняется. Если же идет активная торговля опционами и поза постоянно меняется — никуда не уйти от того, чтобы прогнозировать, как будет меняться сама улыбка.

Например, можно было бы оформить прогноз вот так: центр новой улыбки (при новом значении БА) скользит по текущей:


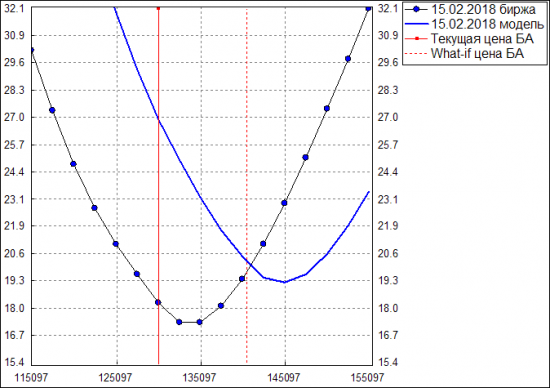
Если поторговать в реале, предполагая такие изменения улыбки, то корреляция эквити с БА становится уже гораздо меньше. Правда, сразу возникает проблема: какое изменение БА брать для расчета дельты? А то бывают ситуации, когда для маленького шага по БА была положительная дельта, а для большого — отрицательная:


И какую дельту тут брать? Ведь БА может изменяться и по чуть-чуть, а может сразу скакнуть большим гэпом. Кроме того, модель перекатывания новой улыбки по старой — это все-таки «пальцем в небо». С точки зрения математики более правильно было бы взять историю улыбок с ftp биржи:


Отфильтровать соответствующим образом и посмотреть, как меняются параметры улыбки при изменении БА. Вот, например, облако зависимости параметра А (отвечает за то, где находится центр улыбки IV) для Ri:

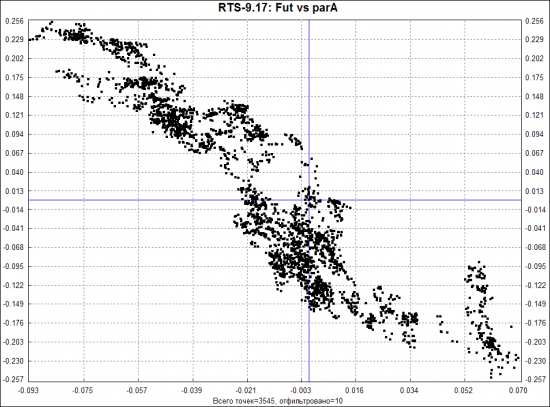
Из этой картинки видно, что IV на центре падает при росте Ri, и растет, когда падает Ri. Выявив такие зависимости для каждого параметра улыбки, мы смогли бы прогнозировать, как будут меняться эти параметры для любого изменения цены БА. И по волшебной формуле биржевой улыбки можно точно вычислять новую улыбку. Но… к сожалению, в реальности даже для параметра А не всегда наблюдаются такие четкие корреляции. Это я просто подобрал картинку покрасивше. Для других параметров вообще — зависимости если и есть, то очень смутные. Т.е. даже применив строгий математический подход, мы не сможем однозначно спрогнозировать изменения улыбки. Можно говорить только о некоем множестве возможных улыбок. Отсюда вывод:

Не существует одной единственно правильной дельты!

Т.е. нужно быть готовым, что дельта у позиции может оказаться и положительной и отрицательной. И искать можно только некую среднюю дельту.

Вот тут, собственно, у меня и возникла идея использовать распределение вероятностей, где окажется цена БА на экспирацию. В качестве такого распределения можно взять рыночное (соответствующее текущим ценам на рынке) или какое-то свое, если не согласны с рынком. Можно гипотетически добавлять-убавлять фьючерса в позицию и, используя распределение, считать различные хар-ки получившихся поз:



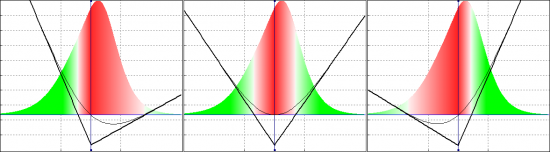
Например, можно посчитать матожидание (МО) PnL получившейся позиции по формуле:


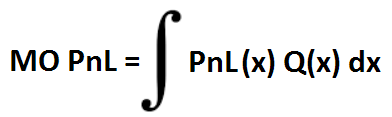
(PnL(x) — PnL на экспирацию, Q(x) — функция плотности распределения вероятностей.)

И посмотреть — при какой добавке получилось максимальное МО PnL. Но оказалось, что как бы мы не вертели фьючом позу — общее МО совершенно не меняется от этого. И если внимательнее посмотреть на формулу подсчета МО, то становится понятно, что это так и должно быть. Если мы добавляем в позу фьюч по текущей цене БА, то на общем МО это никак не скажется, поскольку матожидание распределения = текущей цене БА (если используем рискнейтральное распределение). Так что, первоначальная идея провалилась. Но зато заметил, что если считать МО отдельно по левой половине распределения и по правой, то получаются разные значения. Вот анимашка  — как меняется позиция и ее характеристики в зависимости от того, сколько добавили или убавили фьюча. Хорошо видно, как «наливается» прибылью то левая половина распределения, то правая.

Построил график, на котором по оси X — гипотетическая добавка фьючей в позицию (отрицательные значения — продали фьючи, положительные — купили), а по оси Y — МО PnL:

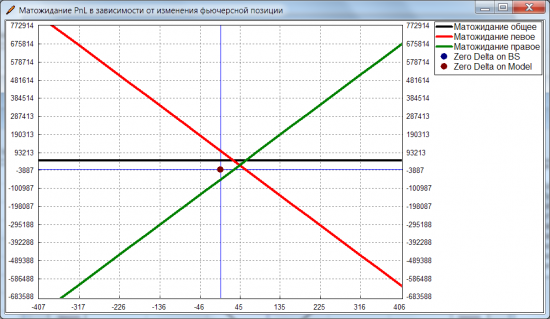
Черная горизонтальная линия — это общее МО позиции. Видно, что оно постоянно вне зависимости от того, сколько мы добавили фьюча в позу. А вот МО, посчитанное отдельно по левой половине распределения (красная линия) и по правой (зеленая) — очень даже зависят. Если продадим очень много фьюча, то MO PnL по левой половине будет сильно положительным, а по правой — сильно отрицательным. Если наоборот возьмем в лонг очень много фьюча, то уже МО по левой половине станет сильно отрицательным, а по правой — сильно положительным. И есть некоторая равновесная точка, в которой эти МО будут равны. И если мы занейтралимся в соответствии с этой точкой (продадим или купим столько фьючей, чтобы МО лев = МО прав), то у нас получается нейтральность не в классическом понимании (касательная к текущему профилю PnL с нулевым наклоном), а в альтернативном. Сформулировать, наверное, можно так:

Позиция занейтралена, если УСРЕДНЕННО нам все равно, куда пойдет БА — вверх или вниз.

Т.е. мы соглашаемся, что иногда перед очередным дельтахеджем можем получить убыток (маленький или большой), иногда прибыль (маленькую или большую). Но в _среднем_ финрез будет одинаковый: что при падении БА, что при росте.

На следующей картинке дельта выровнена в соответствии с равенством левого и правого МО:

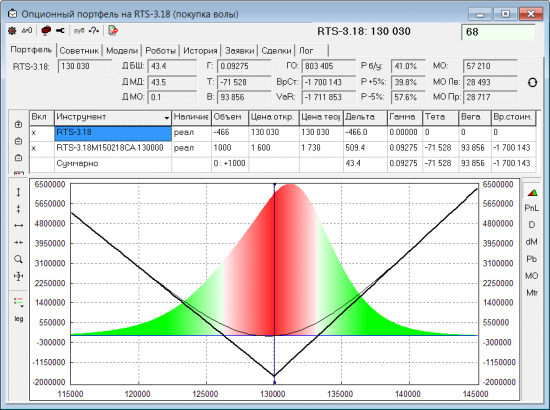
Дельта по БШ тут = 43. Т.е. БШ нас убеждает, что с ростом БА поза будет приносить прибыль, а с падением — убыток. Но БШ ведь не учитывает, что IV будет меняться. И если бы мы выровняли дельту по БШ, то для Ri обнаружили бы почти 100% отрицательную корреляцию эквити с БА (БА растет — PnL падает, БА падает — PnL растет). Вполне возможно, что в данном случае дельта через МО показывает более правильное значение, чем БШ.

Заметил еще интересную особенность этого подхода. В нем есть зависимость от того, какая накоплена PnL к текущему моменту у позиции. При классическом подходе такой зависимости нет. Дельта никак не изменится — поднимем мы позу вверх или опустим. А при подсчете через МО PnL — зависимость есть. Особенно хорошо это видно на примере зигзага. Вот две картинки одной и той же позы, но с разным накопленным PnL:

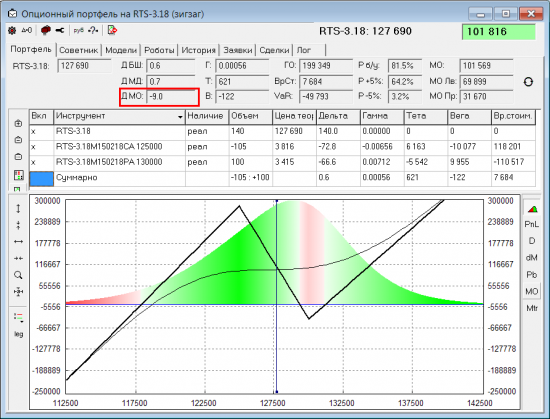
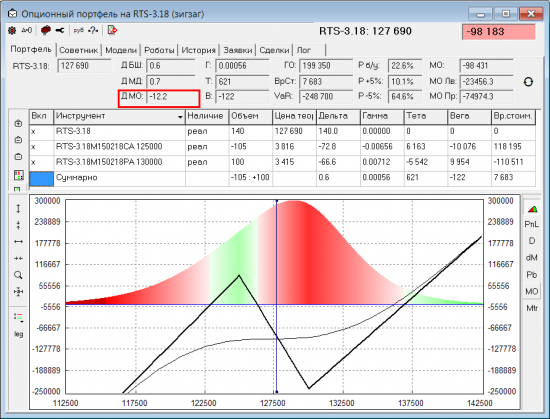
Видно, что в классическом понимании дельта у них одинаковая. Но дельта посчитанная через равенство МО PnL по левой и правой половине распределения — будет слегка отличаться (у первой позы ДельтаМО=-9, у второй -12). Отсюда неожиданный вывод:

Нейтральность зависит не только от самой позиции, текущей улыбки (распределения вероятностей) и прогноза, как они будут меняться, но и от накопленного PnL у позы.

Вот такой альтернативный подход к дельта-нейтральности получился. Интересно, кто что думает по поводу такого способа считать дельту?


P.S. Кстати, теоретически, этот метод можно не только для дельта-нейтральных стратегий применять, но и для направленной опционной торговли. Например, открываем оптимальную опционную позицию соответствующую нашему вью, и с помощью фьючерса поддерживаем комфортное для нас соотношение МО PnL в благоприятную и неблагоприятную сторону.


P.P.S. А может кто из старших товарищей поделится своим подходом к нейтрализации позы фьючом? Прошедшим, так сказать, «огонь, воду и медные трубы» :)