Платформа OptionSmile. Часть 1. Методика оценки справедливой стоимости опционов
Всем добрый день.
После анонса системы OptionSmile на Smart-Lab’e мне стали поступать запросы на слайды презентации, по которым было записано видео. Я понимаю, что не все могут себе позволить тратить время на просмотр, и легче иногда глазами пробежать текст в своем темпе, чем слушать длинные и не всегда зажигательные лекции.
Поэтому я все же решил сопроводить видео-описание подхода текстовыми постами. Это первый из них, посвященный теоретической базе нашего подхода по расчету справедливых цен опционов. Всегда можно посмотреть видео, там информации несколько больше.
Итак, начнем с краткой теории. Fair Value любого актива — это все будущие денежные потоки от него, приведенные к текущему периоду дисконтированием. Если денежные потоки не известны достоверно, а как правило это так, то они должны быть еще взвешены по вероятности их получения.
Для любого дериватива с одним сроком экспирации (фьючерса, свопа, опциона и т.д.) Fair Value считается проще — это все возможные его стоимости на дату экспирации, взвешенные по их вероятности и приведенные к текущему периоду. Поскольку цена дериватива на экспирации всегда однозначно определяется ценой базового актива и некоей формулой, то и за вероятности можно принять вероятности достижения базовым активом (БА) тех или иных уровней.
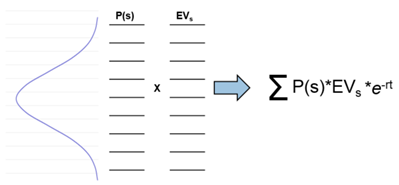
Итого, справедливая стоимость любого дериватива оценивается по формуле:
P(S) – вероятность финиширования БА в определенном значении s
EVs – стоимость дериватива на момент экспирации при значении БА равному s
e-rt – дисконтирующий множитель
Fair Value любого опциона считается еще проще. Мы можем разделить все состояния на момент экспирации на 2 части: в деньгах (ITM, in-the-money) и вне денег (OTM, out-of-the-money).
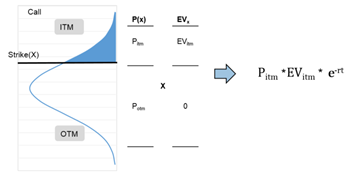
Пример для call-опциона:
Поскольку стоимость опциона при экспирации OTM равна 0, то все вероятности цен базового актива в зоне OTM нас не интересуют, т.к. умножаются на 0.
Итого, FairValue опциона равна:
вероятности экспирации «в деньгах» (Pitm),
умноженной на ожидаемую стоимость опциона пр этом (EVitm) и
приведенной к текущему моменту (e-rt)
причем опциона любого типа. Например, для бинарных опционов все еще проще: EVitm– константа и остается только оценить вероятность экспирации ITM.
С формулой, вроде, понятно. Теперь вопрос на миллион долларов: как оценить Pitm и EVitm? В общем-то нам нужно как-то спрогнозировать распределение базового актива. Возможны 2 подхода:
Подход 1. Параметрический
Здесь мы предполагаем какую-то модель случайного процесса цены БА и подбираем функцию распределения его доходности. Например, в подходе Блэка-Шоулза (БШ) предполагается Геометрическое Броуновское Движение и берется логнормальное распределение доходностей БА. Затем оба параметра (Pitm и EVitm) выводятся из этой модели. Там, например, коэффициент N(d2) как раз и есть наша Pitm. С EVitm чуть сложнее, но тоже имеет однозначную формулу:
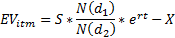
Т.е. формула БШ тоже легко приводится к нашей: Pitm * EVitm*e-rt. Да и вообще, там заложена та же логика, когда рассчитываются переменные d1 и d2. Я еще, думаю, отдельно напишу об этом.
Какие проблемы несет за собой параметрический подход я немного затронул в этой части видеопрезентации. Главное – это балансирующий параметр – σ, который вбирает в себе все ошибки модели и заставляет график вмененной волатильности «улыбаться».
Подход 2. Непараметрический (подход в OptionSmile)
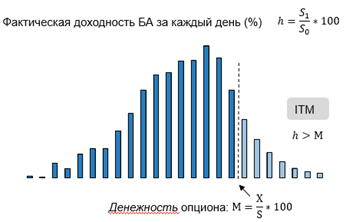
Здесь мы не предполагаем никакой мат.модели распределения доходностей БА, т.е. нам не нужна никакая формула функции плотности распределения (PDF). Все что, мы делаем – это анализируем фактическое распределение БА за прошлый период.
Берем денежность опциона (Moneyness) как отношение страйка к цене БА в процентах и считаем, как часто в прошлом БА «перелетал» эту денежность (оценка Pitm) и как далеко он при этом «залетал» (оценка EVitm).
Получаем две простые формулы:
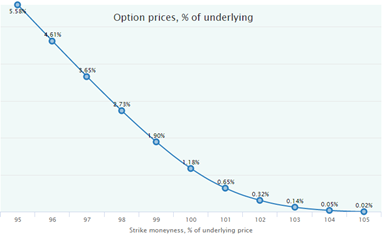
И так по каждому страйку и экспирации можно рассчитать эти пары коэффициентов и построить график таких статистически справедливых цен. Вот такой, например (это уже скриншот из и системы):
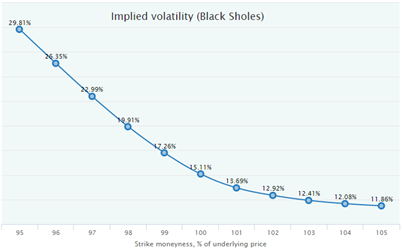
И можно по формуле БШ из этих цен вывести улыбку (точнее ухмылку) Implied Volatility, хотя практического смысла в этом не много:
Да и вообще, можно взять любую функцию распределения БА и попробовать откалибровать ее под полученную цену опционов. Логнормальная функция в подходе БШ, пожалуй, самая простая, вот и стала популярной: нужен-то всего один параметр — σ.
Итак, «справедливость» такой цены нам говорит о том, что если бы в прошлом сделки заключались именно по этим ценам, то и у покупателя, и продавца в итоге была бы нулевая прибыль (без транзакционных затрат). Т.е. все было бы «справедливо»: вся сумма полученной премии продавцом компенсировалась бы убытками в случаях экспирации ITМ, а все, что заплатил покупатель за опционы, вернулось бы ему точно такой же прибылью при ITM случаях.
Теперь не менее справедливый вопрос: ок, с прошлым понятно, но точно ли все это можно экстраполировать в будущее? Повторится ли прошлое в будущем?
Пожалуй, это еще один вопрос на миллион долларов!
На него отвечает раздел в презентации, посвященный фильтрации рыночных режимов. Я опишу его текстом в следующем посте.
Также в следующих постах расскажу о расширенной функциональности системы:
- оценке доверительных интервалов для Fair Value
- расчете исторических котировок для большей статистической значимости
- матрицах опционных спред-стратегий
Если вам интересен подход, заходите на наш сайт, регистрируйтесь, пробуйте. Все бесплатно, проект некоммерческий.
Также вступайте в группу на Facebook. Там, как наберется компания, начнем обсуждения.
И, если кому не трудно, поставьте плюс этому посту. А то, на Smart-Lab’е я человек новый. Только недавно понял, что с начальным рейтингом почти ничего делать не могу. Даже посты и то по 1 в день могу размещать.
Кирилл Браулов, наконец дошли руки. Отвечаю.
Подход, который я применяю используется еще много где. Самое очевидное, в страховании. Если упрощенно: справедливая страховая премия равна вероятности страхового случая, умноженная на ожидаемую сумму страховой выплаты. По облигациям аналитики считают справедливый спред над безрисковой ставкой как вероятность дефолта, умноженную на ожидаемую сумму потерь (loss-given-default). И много еще где, где нужна стоимость риска. Во всех случаях пока ничего лучше не придумали, как оценивать оба компонента этой стоимости исходя из исторических (эмпирических) данных.
Да, эмпирические данные дадут один единственный путь, но еще и дадут оценку вероятностей на будущее. По сути, они дадут функцию плотности вероятности. Конечно, крайне редко актив придет ровно в точку с мат.ожиданием или медианой. Но, если много раз это повторять, то будет стремиться. Т.к. все тут стохастическое, то для реальной торговли нужно иметь приличную, статистически значимую разницу между справедливой и рыночной ценами. Страховые компании тоже не справедливую стоимость просят за страховку, у них есть повышающий коэффициент — loading.
Еще я пришел к тому, что брать эмпирические данные просто за какое-то окно в прошлом – неправильно. Это то же самое, что, например, узнав за окном температуру воздуха (скажем, +5), сравнить ее со средней температурой за последние полгода и сделать вывод «тепло» на улице или «холодно». Разумеется, нужно сравнивать со средней температурой в этом конкретном месяце, городе, и времени суток. Для Сочи в мае +5 будет холодно, а для Мурманска – жарко. Для января – это оттепель, а для июля – похолодание. Еще раз напишу мой главный тезис: экстраполируем только то прошлое, которое похоже на настоящее. Собственно, основная сложность – идентифицировать правильный режим и отобрать данные из прошлого. Нужна правильная фильтрация прошлого.
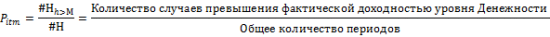
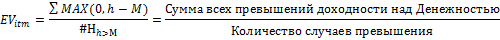
Спасибо за такой подробный ответ. Насчет страхования, возможно там случайные процессы — стационарные или почти. В финансах же процессы совсем-совсем нестационарные. Или — не согласны?
Вполне возможно, что взяв одну случайную траекторию _стационарного_ случайного процесса (т.е. с постоянным МО, постоянной дисперсией и т.д.) можно примерно восстановить сам случайный процесс (и как следствие — построить распределение вероятностей). Но вот чтобы из одной случайной траекторию _нестационарного_ процесса восстановить весь случайный процесс (у которого даже близко нет постоянного МО, да и дисперсия/асимметрия/эксцесс постоянно меняются) — имхо, это невозможно.
Насчет фильтрации, так понимаю, что находите кусок истории, который похож на текущий рынок, считаете что этот кусок = стационарный, и что в ближайшем будущем движения цены будут соответствовать этому стационарному случайному процессу. Очень сомнительные предположения. И чем-то похоже на попытки линейных торговцев найти волшебный грааль, который будет им подсказывать, что в одни моменты надо торговать трендовые стратегии, а в другие — контртрендовые. Думаете, такой грааль существует?
Думаю, в страховании тоже все далеко от стационарности. Согласитесь, когда выпадает первый снег процесс генерации страховых убытков а автостраховании ну совсем не такой, как, скажем в августе. Вообще, там все более продвинуто, чем в опционах. Несколько другой подход к случайному процессу генерации убытков (через Пуассона, например).
Нестационарность пытаюсь уменьшить фильтрацией. Известно, что волатильность кластеризуется. Плюс еще можно искать разные кластеры в виде режимов рынка (примеры в постах).
Про фильтрацию не совсем так. Не «кусок» истории, а конкретные даты со схожей IV опционов (VIX), на схожем макро-цикле (бычий, медвежий рынки) и в схожем краткосрочном цикле (тех.индикаторы). Это будет не один кусок, а разбросанные по истории дни, после которых и MO и сигма будут довольно устойчивы.
Два таких режима я считаю, что четко нашел (RSI < 45 и MACDh > 0.2%) есть в видео.