Поиск идеального плеча или что такое оптимальное "f" (Ральф Винс "Математика управления капиталом")

Друзья, привет!

Большинство наверное прекрасно знает, что плечо на фондовом рынке и плечо друга — две разные вещи! И со многими, я уверен, фондовое плечо ни раз играло злую шутку! Не буду оригиналом и скажу, что и я неоднократно становился заложником агрессивных плеч, в следствии которых мне ни раз приходилось нести несоизмеримые потери по счету.

Понимание того, что плечи нужно сокращать пришло естественно не сразу. Переломным моментом, как я уже писал в одном из своих постов, стал просмотр видео с участием Алексея Каленковича (ещё раз отдельное ему за это спасибо).

Кто еще не видел это видео, то вот оно:

vimeo.com/25638210

В этом видео Алексей рассказывает о его понимании книги Ральфа Винса «Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров».
На мой взгляд, книга достаточно сложна для понимания, по крайней мере, с первого раза. В книге достаточно много разного рода приблуд. Главной же идеей данной книги является поиск так называемого «оптимального f». По нашему — оптимального плеча, при котором достигается максимизация долгосрочной доходности с оптимальным риском.

Теперь о самой книге.

 В книге «Математика управления капиталом» Ларри Вилльямс описал метод фиксированной фракции. Фиксированно-фракционный метод основан на том, что в каждой сделке можно рисковать суммой, не превышающей заранее заданного процента от текущего баланса сче­та. По мере роста размера счёта происходит пропорциональное увеличение размера позиции. Применительно к построению торговых систем для разного рода рынков, размер процента риска необходимо привязывать не только к размеру торгуемого лота, но также ещё к значению используемого плеча, уровню стоп-лосса, заданному в системе, а также торгуемому инструменту. Другими словами необходимо учитывать количество потенциально теряемых в сделке пунктов и их стоимость на данном инструменте.

Достоинством фиксировано-фракционного метода является относительная простота и прозрачность, поскольку объем позиции вычисляется пропорционально размеру депозита. Риск остается постоянным на протяжении всей торговли. При этом полученная прибыль автоматически реинвестируется при вычислении размеров лотов последующих сделок.

Главным недостатком фиксировано- фракционного метода является эффект «ассиметричного рычага». Суть этого эффекта в том, что для компенсации потерь, понесенных в сделке, вам необходимо заработать в пунктах больше, чем вы потеряли. Этот дисбаланс проявляется тем сильнее, чем агрессивнее торговля, чем больше процент риска в каждой сделке. Происходит это потому, что отыгрываться придётся меньшим лотом, тем лотом, который позволит вам оставшийся после убытка депозит. Эффект ассиметричного рычага поясняется следующей таблицей.



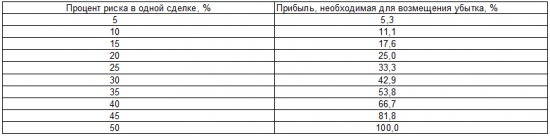
Из таблицы следует, что при малых рисках (5…10%) вам необходимо заработать почти столько же (5,3…11,1%), чтобы покрыть убыток. При риске 50% необходимо заработать в 2 раза больше (100%), чтобы выйти на прежний уровень.

Фиксированно-Фракционный метод имеет несколько разновидностей:

Метод оптимальной фракции (оптимальной f).

Оптимальная фракция определяется как фик­сированная фракция, которая дает больший доход, чем любая другая фиксированная доля, применяемая в рамках данной торговой стратегии. Например, для гипотетической торговой системы с шансами 50% выиграть $2, против 50% проиграть $1 в каждой сделке больше всего прибыли можно получить, если прибегнуть к стратегии реинвестиро­вания с оптимальной фракцией (оптимальным риском в каждой сделке), равной 25%. При этом, кривая зависимости полученной в серии сделок прибыли (у Ральфа Винса TWR- Terminal Wealth Relative или «относительный конечный  капитал») от процента риска (величины фракции) близка к нормальному распределению.



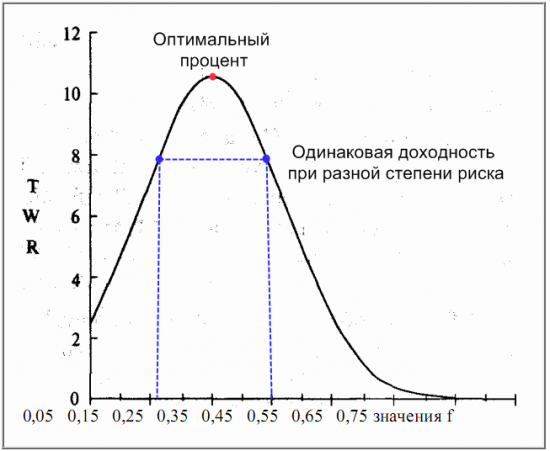
По мере увеличения фракции конечный результат системы  возрастает  до определенного уровня. При размере фракции больше и меньше этого уровня прибыль падает. Таким образом, один и тот же результат может быть достигнут системой при различных размерах фракции (точках, находящихся как на левом, так и на правом скатах кривой), т.е. можно иметь ту же результативность, рискуя меньшей частью капитала. Если вы играете мельче, чем оптимальное f, то ваш риск уменьшается в арифметической прогрессии, а прибыль — в геометрической.

На первый взгляд кажется, что ме­тод может привести к феноменальному росту счета при оптимальном соотношении риска и вознаграждения. Однако методу присущ существенный недостаток, заключающийся в том, что расчёт оптимальной фракции производится  для серии предыдущих торговых сделок. Этот метод не применим для прогнозирования, он обращен в основном на исследование прошлых данных. Допустим, оптимальная фракция для предыдущих 100 сделок составляла 15%, в последующих 100 сделках эта доля может оказаться равной 9%. Если для предыдущих 100 сделок оптимальной была доля 15% и вы решили провести 100 следующих сделок с той же фракцией, то этот процент может оказаться непомерно большим и привести к существенным убыткам.

Метод безопасной фракции (безопасной f).

Появление метода обусловлено большими значениями просадок, присущими методу оптимальной фракции. Допустим, оптимальная фракция для заданной торговой системы составляет 25%, однако дродаун системы с таким риском на исторических данных достигает 80%. Такие просадки выдержать психологически нелегко, особенно при игре крупными суммами. В отличие от метода оптимальной фракции в данном методе расчёт фракции производится исходя из максимального проседания счёта. Работа по методу безопасной фракции менее рискованна, чем при использовании оптимальной фракции, но и прибыль в результате будет существенно меньше, а рост капитала будет проходить медленнее.

Расчет фракции производится на основе заданного процента просадки, которую трейдер психологически может себе позволить. Если, например, приемлемой считается  просадка в 25%, берём максимальный исторический дродаун системы и, исходя из него, рассчитываем процент риска в каждой сделке, например 5%. Как правило, это значение существенно меньше оптимальной фракции.

Метод безопасной фракции позволяет определиться с приоритетами и решить, что важнее– большая  прибыль ценой большего риска и просадок или наоборот, относительно безопасная торговля за счёт потери части прибыли.

Теперь пример, который в своей книге приводил Ральф Винс, и формулы.

Допустим, мы подкидываем идеальную монетку, с вероятностью выигрыша и проигрыша 50 на 50. Предположим, что в случае выигрыша мы получаем 2 доллара, а в случае проигрыша теряем 1 доллар. Математическое ожидание тогда такой игры будет (0.5*2)+(0.5*(-1)) = 0.5. Т.е. имеем положительное ожидание, 50 центов за бросок.
Проведем  серию из 40 сделок и представим результат в виде графика, где по  оси абсцисс будет значение оптимального f, а по  оси ординат — показатель TWR. (рисунок выше).

TWR –это показатель, характеризующий относительный конечный капитал, или,  проще говоря, то, во сколько раз мы увеличили наш изначальный депозит.
При отклонении оптимального f всего на незначительные величины резко меняет значение TWR, что отражается на кратном изменении потенциальной прибыли.

Расчет оптимального F: Для расчета оптимального f необходимо сначала вычислить прибыль за определенный период — HPR, которая рассчитывается по формуле: HPR=1+f*(-сделка/наибольший проигрыш), где:

• f — доля капитала;
• -сделка — прибыль или убыток в этой сделке  (с противоположным знаком, чтобы  убыток стал положительным числом, а прибыль — отрицательным)
• Наибольший проигрыш — наибольший убыток за сделку (это всегда отрицательное число)