16 декабря 2016, 16:00

Случайность, Эффективность и ТехАнализ.

Для грамотных математиков любящих графики случайного блуждания, распределения приращений и кибернетикам с априорными гипотезами без доказательств.

Сжатие данных - алгоритмическое преобразование данных, производимое с целью уменьшения занимаемого ими объёма, за счет устранения избыточности, содержащейся в исходных данных — повторяющихся последовательностей и значений.

Случайные сигналы, процессы, последовательности, белый шум не обладают свойством избыточности. Сжатие данных принципиально невозможно без потерь.

Гипотеза — если колебания цен есть случайный процесс то сжатие данных последовательности приращений не возможно и коэффициент сжатия не должен превышать 1.

Условия испытаний.
— Взяты часовые приращения за 2015-2016г.г.
— На каждое приращение выделено 2 байта для минимизации исходных данных и чистоты эксперимента.
— Для каждого инструмента сформирован файл размером 2 байта х кол-во приращений.
- что бы не изобретать велосипед файлы были заархивированы программой WINRAR.

Результат испытаний.

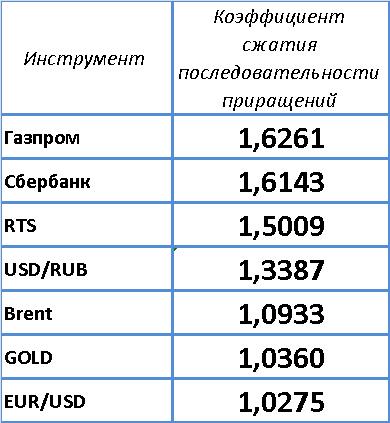
Все последовательности были успешно сжаты.

ВЫВОД — ГИПОТЕЗА НЕВЕРНА. Колебания цен НЕСЛУЧАЙНЫ, а имеют закономерности, повторяющиеся последовательности и тенденции.
Соответственно изменения цен могут быть прогнозируемыми с помощью технического анализа.

Конец.

технический анализ случайные процессы случайное блуждание алгоритмы

Маркин Павел

Санкт-Петербург

274

10 249

с 6 июля 2016

95 Комментариев

Маркин Павел
16 декабря 2016, 16:01
А. Г. А так?
0
А. Г.
16 декабря 2016, 16:03
Вообще то случайность — это когда наше лучшее знание о будущем, это набор событий с разными шансами их появления, как минимум два из которых ненулевые. Доказательством отсутствия случайности каких-либо последовательно происходящих событий может быть только построение точного прогноза всех этих событий ДО их появления.
+2
- Reshpekt Fund Russia ☮
  16 декабря 2016, 16:13
  А. Г., движения цен предопределены некими входными параметрами, при кажущейся случайности и непредсказуемости система детерминирована, просто нет аналитического аппарата. чтобы всё обсчитать. В человеческой терминологии случайно, но не случайно же, тем более нам точный прогноз не нужен, достаточно, если линеаризация даст указание на направление, куда оно всё скорее всего двинется… ;-)
  +1
  - А. Г.
    16 декабря 2016, 16:16
    Reshpekt Fund Russia, совершенно неважно, что мы предсказываем — направление или точное значение. Все вышесказанное относится к прогнозу направления: можно его точно предсказать или нет.
    0
    - Reshpekt Fund Russia ☮
      16 декабря 2016, 16:29
      А. Г., хм, а тренды тогда что? 50% вероятность?
      0
      - А. Г.
        16 декабря 2016, 16:34
        Reshpekt Fund Russia, а нет общепринятого определения «тренда». Для каждого «определения» мы можем получить долю встречаемости на случайном блуждании и уже «плясать» от отличия от этой доли в наблюдаемом процессе. А при статистическом совпадении долей и говорить нечего.
        0
        Reshpekt Fund Russia ☮
        16 декабря 2016, 16:46
        А. Г., ну я не про определение, а про персистентность. Само великое троединство: тренд, бифуркация, контртренд говорит о детерминированости. Нелинейный процесс линеаризуется паттернами, тем же теханализом, остаётся только сделать ставку на то, что вероятнее всего (тренд начался и продолжится). Точный прогноз цены или ещё чего такое же точное не нужны.
        +1
        А. Г.
        16 декабря 2016, 16:51
        Reshpekt Fund Russia, ну вообще то корреляция по модулю меньше 1, уже означает отсутствие точной линейной взаимосвязи, а отдельных случаях (многомерная нормальность) является необходимым и достаточным условием случайности. А ведь корреляцию существенно больше нуля считают свидетельством персистентности, а на точную связь указывает только одно ее значение — 1. В данной дискуссии мы вроде не искали ответ на вопрос: можно ли зарабатывать с положительным МО? А дискутируем относительно другого вопроса: можем ли точно знать что-то об этом МО с уверенностью в 100%?
        0
        Reshpekt Fund Russia ☮
        16 декабря 2016, 16:54
        А. Г., 0,5 < Н < 1,0 же.
        0
        А. Г.
        16 декабря 2016, 16:57
        Reshpekt Fund Russia, H вообще то плохой показатель для нестационарного случая вообще непонятно что показывающий. Но это так, немного «в сторону». Но для стационарного случая такое неравенство как раз указывает на наличие случайности.
        0
        nwtour
        16 декабря 2016, 17:24
        Reshpekt Fund Russia, Часто бывает что на разных таймфреймах бывает контртренд и тренд одновременно. Как можно говорить о существовании того что изменяется на противоположное в зависимости от формы отображения? Технический анализ это просто форма отображения информации, фильтр. Тренд-контртренд это просто словечки для описания СОБСТВЕННОГО восприятия рынка и к реальному распределению вероятностей не имеют.
        0
        Reshpekt Fund Russia ☮
        16 декабря 2016, 17:41
        nwtour, это не важно на каком тренде и в какую сторону, важна устойчивость/закономерность, следствием этой устойчивости будет ставка трейдера на том фрейме/фреймах, на которых распознан тренд, выигрывшая ставка упадёт в копилку, количество выигравших ставок даст посчитать вероятность, если годами ставка на тренд приносит выигрыш, вопрос закрыт с вероятностью. Если же плясать не от печки (не от трейдера и его фильтра восприятия), то тут задача совершенно другого толка, появляется Хёрст, появляется проблематика терминологии (что есть тренд), как там РЕАЛЬНО распределяются вероятности, и вероятности чего, я не знаю, пусть математики лоб морщат.
        0
- Маркин Павел
  16 декабря 2016, 16:16
  А. Г., точный прогноз можно построить на основе выявленных закономерностей, которые являются избыточной информацией в последовательности.
  0
  - А. Г.
    16 декабря 2016, 16:17
    Маркин Павел, вопрос можно или нет точно предсказать в случае отсутствия точного прогноза - это вопрос веры, а не знания.
    0
Reshpekt Fund Russia ☮
16 декабря 2016, 16:06
Соотвественно ГСЧ генерирует нечто похожее, но не рынок?
0
Igr
16 декабря 2016, 16:06
а не говорит ли это, что чем ближе коэффициент сжатия к 1 тем, более не предсказуем процесс, или более эффективен данный инструмент?
+1
- Маркин Павел
  16 декабря 2016, 16:11
  Igr, да чем меньше коэффициент тем более эффективен инструмент и изменения его случайны
  +2
  - Igr
    16 декабря 2016, 16:15
    Маркин Павел, а не могли бы вы привести расчёты для большего количества акций? ну хотя б для тех на кого есть фьючи, интересны результаты
    0
А. Г.
16 декабря 2016, 16:15
Поясню на примере из той же дискуссии. Если в результате 250 независимых бросаний монетки выпало 200 орлов, то мы можем утверждать, что с большой вероятностью монетка кривая и шансы выпадения орла гораздо выше решки, но в силу той же независимости мы не сможет точно предсказать, что на следующем испытании выпадет орел, а лишь можем констатировать то, что сформулировано выше.
+2
- Маркин Павел
  16 декабря 2016, 16:19
  А. Г., но мы можем предсказать что на последующих 25 бросаниях будет ~ 20 орлов, что предопределяет выигрыш.
  0
  - А. Г.
    16 декабря 2016, 16:31
    Маркин Павел, это говорит лишь о большой вероятности выигрыша при ставке на орла, но не отменяет случайности этого выигрыша.
    0
Press
16 декабря 2016, 17:00
можете скрин открытого файла показать, который вы жали?
0
- Маркин Павел
  16 декабря 2016, 17:10
  Press,
  
  0
  - Press
    16 декабря 2016, 17:17
    Маркин Павел, исходный имел ввиду
    0
nwtour
16 декабря 2016, 17:05
Различная энтропия последовательностей газпрома и usdeur ну никак не означает что данные последовательности формируются неслучайными процессами.
Одна и та же функция генерирующая случайную последовательность может сформировать как ряд с высокой энтропией так и низкоэнтропийный ряд с равной вероятностью.
+2
Тимофей Мартынов
16 декабря 2016, 17:08
Чувак, ты гений!
Я прям охренел от такого нестандартного подхода!
прикольно получилось

причем я думаю, реально вывод относительно EURUSD получился в точку!
+2
- Маркин Павел
  16 декабря 2016, 17:15
  Тимофей Мартынов, Вывод чем больше участников и больше ликвидность тем менее эффективен инструмент.
  +1
Машковский Евгений
16 декабря 2016, 17:16
По идее все процессы случайные, потому как простой прогноз протянуть руку и взять стакан, может не сбыться, ибо за это время можно успеть вдруг протянуть ноги, прилетит метеорит, внутреннее напряжение стакана его разрушит… и со 100% вероятностью нельзя сказать, что прогноз сбудется, другими словами это случайность!
0
- nwtour
  16 декабря 2016, 17:32
  Машковский Евгений, Все верно. Если человеку предложить игру — тебе дают монету за то что ты делаешь самое популярное действие, а если не угадал то забирают. То распределение между людьми которые «протянули руку и взяли стакан» и «одёрнули руку» станет случайным и примерно равным 50%.
  0
- Reshpekt Fund Russia ☮
  16 декабря 2016, 17:49
  Машковский Евгений, тогда так. Два трейдера ставят свои противоположные ставки на то, что ты будешь каждые 5 секунд протягивать руку и брать стакан. Один ставит 100 долларов на то, что ты возмёшь, а второй (математик) 100 долларов на то, что не возьмёшь (внутренне натяжение, смерть, метеорит). Кто там разбогатеет через пару часов на такой случайности?
  0
  - Машковский Евгений
    16 декабря 2016, 17:52
    Reshpekt Fund Russia, Думаю математик будет считать, что не известно, ибо случайно, а противник, думаю этот вечер не забудет никогда!))))))))
    +1
    - Reshpekt Fund Russia ☮
      16 декабря 2016, 17:55
      Машковский Евгений, ))) точно. Постоянно берущийся стакан — это тренд, а математик — это сливающий против тренда бабло лох ибо думает, что всё случайно, хаос, броуновское движение, никаких перекосов вероятности, никакой детрминированности, подумаешь, 20-ый раз взял, скоро метеорит прилетит.
      +2
      - Машковский Евгений
        16 декабря 2016, 17:57
        Reshpekt Fund Russia, ))))))))))
        0
Press
16 декабря 2016, 17:33
«Гипотеза — если колебания цен есть случайный процесс то сжатие данных последовательности приращений не возможно и коэффициент сжатия не должен превышать 1. »

"Коэффициент сжатия — основная характеристика алгоритма сжатия. Она определяется как отношение объёма исходных несжатых данных к объёму сжатых, то есть: $k=\frac{S_o}{S_c}$ , где k — коэффициент сжатия, S_o — объём исходных данных, а S_c — объём сжатых. Таким образом, чем выше коэффициент сжатия, тем алгоритм эффективнее. Следует отметить:
- если k = 1, то алгоритм не производит сжатия, то есть выходное сообщение оказывается по объёму равным входному;
- если k < 1, то алгоритм порождает сообщение большего размера, нежели несжатое, то есть, совершает «вредную» работу."
+2
- Маркин Павел
  16 декабря 2016, 17:51
  Press, Вы развёрнуто повторили то что я написал, забыли только скопировать, что
  Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или белый шум, зашифрованные сообщения), принципиально невозможно без потерь.
  0
Displacer
16 декабря 2016, 17:42
А если взять для хранения «приращений» три байта, то рынок станет еще более неслучайным. Я уж промолчу, что будет, если взять int32_t или int64_t. В общем постановка эксперимента не то что бы некорректна, но требует отдельного обоснования в части размера данных.

PS: для тех, кто не понял — поясню, в данных могут присутствовать биты/байты, которые не несут информации, и поэтому будут сжиматься в десятки раз.
+2
- Маркин Павел
  16 декабря 2016, 17:48
  Displacer, в один байт приращения без потерь точности не уместить, соответственно 2 байта минимально необходимый размер. а три и более это преднамеренная фальсификация результата.
  0
  - Displacer
    16 декабря 2016, 17:50
    Маркин Павел, вообще то количество байт не обязано быть целым это раз. Во вторых, приращения на рынке изначально имеют минимальное фиксированное приращение, задаваемое биржей. Т.е. данные требуют нормализации.
    +1
    - Маркин Павел
      16 декабря 2016, 18:34
      Displacer, у меня, как бывшего программиста под DOS, минимизация использования ресурсов памяти, идёт на генетическом уровне ;)
      0
  - Displacer
    16 декабря 2016, 18:28
    Маркин Павел, короче, скорее всего вы данным экспериментом выяснили, во сколько раз надо сократить размер данных ;) Т.е. приблизительно надо полтора байта :)
    0
- Press
  16 декабря 2016, 17:49
  Displacer, «поясню, в данных могут присутствовать биты/байты, которые не несут информации,» — ты мой ГЕРОЙ!
  
  +1
Cristopher Robin
16 декабря 2016, 18:09
Методология эксперимента вызывает сомнения. Во-первых, нужно применять кодирование данных во всех случаях, иначе возникает избыточность связанная с хранением данных определенного типа. Во вторых, нужно строить разные выборки с разным количеством данных и смотреть. В третьих, не хватает того же самого коэфициента для случайного блуждания желательно разных типов для того чтоб удостоверится, что исходная гипотеза верна и сжатие случайного блуждания реально показывает 1.
+1
Борис Гудылин
16 декабря 2016, 18:49
Больше года наблюдаю за дискуссиями с «математическим» уклоном.
Новых мыслей относительно того, что мы изучаем в рынке и какими средствами — не заметил, может пропустил. Правда, сегодня увидел маленький-маленький намек, но он остался без развития. Можно даже было бы сделать генератор вариантов для таких дискуссий, загрузить его чем-то, к устройству рынка отношения не имеющего и запустить.

— Почему вы ищете потерянные ключи под фонарем?
— Потому, что здесь светлее.

Есть такая математическая дисциплина — теория хаоса, ее можно применять к рынку. Один из постулатов — малые изменения в начальных данных могут привести к большим последствиям (многие слышали про «эффект бабочки»). Этот постулат можно попробовать перенести на методологию — немного не то исследуем, немного не тем инструментарием — и на выходе получаем что-то сомнительное. Даже при всей аккуратности в выкладках. Про неаккуратность (математическую) уже не говорю.

Недавно ТС публиковал пост про фрактальную размерность.
Дал известное определение через предел (ПРЕДЕЛ!), а потом привел программу, которая считает эту фрактальную размерность по нескольким свечкам. В чем ошибся тогда ТС?
В том, что связал фрактальную размерность с трендом, в количестве свечек, забыв, что такое предел, в том что не ответил на вопрос про 64 свечки или в том, что не заметил, как Старченко осторожно высказывался относительно своего алгоритма?
Ну, да, есть сомнения. Ну, неаккуратность, сводящая пост в 0.
Но главное было не в этом.

А есть ли смысл применять фрактальную размерность к рынку?

Вопрос на понимание.
Найдите хотя бы 3 причины, делающие такое применение бессмысленным, бесполезным.

P.S. ТС горы бы свернул, определись он точнее с предметом, инструментарием и методологией. А так он просто тратит свое время и фантазию.

С уважением к ТС.

+4
- Маркин Павел
  16 декабря 2016, 19:15
  Борис Гудылин, ТС, уже давно болт забил горы, предмет, инструментарий и методологию. ТС ленится.
  Соответственно ТС старается переложить предварительную работу по отсеву идей на «коллектив». При этом ТС иногда на 90% не согласен с идеями которые описывает, но Ведь «ТС может ошибаться», поэтому ТС занимается провокацией через «неаккуратность»
  ТС ищет что нибудь нестандартное (на его взгляд) и «кидает камушки в озеро понаблюдать за рябью».
  
  по поводу 64 — старая привычка втыкать везде 2^n, мне так проще считать и запоминать.
  +1
  - Борис Гудылин
    16 декабря 2016, 19:23
    Маркин Павел, ну, ладно, я — пытаюсь увидеть во всем двойное-тройное дно, но есть же неокрепшие умы. Они то могут и не разобраться. И долго потом идти во вроде понятную и привлекательную, но сомнительную сторону.
    +3
Изя 3%
16 декабря 2016, 20:52
Рошалю пора открывать хэдж фонд. )
А если пожать сиплого что получится? Да, и втб интересно посмотреть ))
0
bstone
16 декабря 2016, 23:16
Надо входные данные представить двумя потоками: первый поток — число бит в каждом приращении, второй поток — сами приращения без избыточных данных. Сжимать только второй поток. Так будет точнее.
+2
OlegSh5
17 декабря 2016, 07:05
Очень красивый и оригинальный подход.
Но, проблема в том что, вывод не правильный. Приращения сами по себе могут оставаться случайными, при этом модули их — отнудь не случайные величины. Они несут в себе закономерности сохранения волатильности, как суточной так и общей. Именно эту закономерность эксплуатирует винрар, когда хорошо сжимает Газпром (где волатильность легко предсказуема) и тяжело сжимает евродоллар, где волатильность ровная.
+1
MS
17 декабря 2016, 16:00
Для грамотных математиков, любящих ...
Грамотный математик, подставил отсутствующую запятую.
0
- Маркин Павел
  17 декабря 2016, 17:00
  MS, по русскому и литературе было 3
  0
MS
17 декабря 2016, 16:32
Степень сжатия зависит не от случайности, а от распределения приращений. Минимальное сжатие будет у равномерного распределения, гораздо большее — у нормального (например).
+1
- Маркин Павел
  17 декабря 2016, 17:00
  MS,
  Определение случайности по Колмогорову и Мартин-Лефу: чтобы строка была признана случайной, она должна:
  - Быть несжимаемой — компрессия подразумевает поиск представления информации, которое использует меньше информации. К примеру, бесконечной длинная двоичная строка 0101010101…. может быть выражена более точно как 01, повторенное бесконечно много раз, в то время как бесконечно длинная строка 0110000101110110101… не имеет четко выраженного паттерна, а значит ее нельзя сжать до чего-либо короче, чем эта же самая строка 0110000101110110101 … Это значит, что если Колмогоровская сложность больше или равна длина строки, тогда последовательность алгоритмически случайна.
  0
  - MS
    17 декабря 2016, 17:48
    Маркин Павел, здорово. Так и посчитайте значения характеристики Колмогорова, а не WinRar. Снимутся вопросы.
    0
    - Маркин Павел
      17 декабря 2016, 19:39
      MS, 1. Показатель колмогоровской сложности является невычислимой функцией.
      2.Для вычисления верхней границы Показателя колмогоровской сложности применяется любой метод компрессии для исследуемой последовательности.
      0
      - MS
        17 декабря 2016, 21:12
        Маркин Павел, ОК. Утверждение статьи может быть получено множеством других способов. Как ещё одна иллюстрация разве что.
        1. Практического применения нет.
        2. Что понимать под случайностью. Представим модель: двумерное распределение приращений. Направление — биномиальное, размер — Пуассон. Есть подозрение, что коэффициент сжатия будет всегда больше 1, если p<>1/2 в биномиальном. А обе размерности при этом случайны.
        На практике это модель для направленного тренда за 10 лет. Нет ответа насколько он случаен.
        3. Эта модель с p =1/2 и детеминированной функцией размеров приращений тоже невозможно торговать. А сжатие у неё будет близко к 2.
        0
        Маркин Павел
        17 декабря 2016, 21:31
        MS, сгенерируйте обе модели пожалуйста и давайте проверим
        0
        MS
        18 декабря 2016, 12:33
        Маркин Павел, пока не буду этого делать. А продолжу теоретически.
        Итак, пусть знаки приращений распределены биномиально с p=1/2, размеры приращений — константа.
        Алгоритм упаковки: записываем длины серий положительных и отрицательных последовательных приращений.
        Пусть n — количество приращений. Тогда с вероятностью 1-2^(-n) упакованное слово будет короче исходного. Матожидание же коэффициента сжатия — e.
        Если p > 1/2, то это матожидание ещё возрастает.
        
        «О! Мы взяли какой-то алгоритм сжатия, какие-то данные и всегда получаем коэффициент сжатия >1. Данные неслучайны! По Колмогорову!»
        0
        Маркин Павел
        18 декабря 2016, 22:31
        MS,
        Итак, пусть знаки приращений распределены биномиально с p=1/2, размеры приращений — константа.
        
        «О! Мы взяли биноминальное распределение, но распределяем знаки, и получили равномерное дискретное распределение — конечное число значений с равными вероятностями — дискретный белый шум/подкидывание монеты»
        
        Алгоритм упаковки: записываем длины серий положительных и отрицательных последовательных приращений.
        
        «О! мы забыли что, при сжатии в архив добавляется информация для восстановления»
        Так если Вашу последовательность сжимать по Вашему алгоритму, то:
        1. на признак серия/не серия выделяется 1 бит, то коэффициент сжатия = 1/(1+доля несерийных значений) — всегда меньше 1
        2. на признак серия/не серия 2 бита — чтобы коэффициент сжатия был не меньше 1, кол-во несерийных значений должно быть меньше 1/3 от всей последовательности, при условии что все серии будут равны по длине четырём, иначе, что никак не соответствует равномерному дискретному распределению.
        3. дальше только хуже.
        
        Если p > 1/2, то это матожидание ещё возрастает.
        Ну при p=1 это же тоже случайный процесс по Вашему ;)
        
        «О! Мы пукнули мозгом! Так красиво и высокомерно пошутили!»
        0
        MS
        18 декабря 2016, 22:59
        Маркин Павел, мне сложно догадаться к чему Вы эти пункты написали.
        Вот пример результата предложенного алгоритма.
        Последовательность приращений: +d+d+d-d+d-d-d-d-d-d-d+d
        Сжатая строка: +31161
        0
        Маркин Павел
        18 декабря 2016, 23:09
        MS, (+d+d+d-d+d-d-d-d-d-d-d+d) = (111010000001) 12 бит
        (+31161) =(+ (1) 3 (011) 1(001) 1 (001) 6(110) 1 (001) получаем (1011001001110001) 16 бит
        Сжали с приращением на 4 бита — оригинально!
        0
        Маркин Павел
        18 декабря 2016, 23:14
        MS, Лови 10 рандомов, каждый по 800000 битных знаков, попробуй упакуй, ссылка.
        0
bstone
17 декабря 2016, 22:37
В общем, я решил проблему избыточности кардинально, выдавая в битовый поток только знак приращения.

Понятно, что будет небольшой перекос из-за того, что нулевые приращения нужно приравнять либо к 0, либо к 1. Чтобы уменьшить его влияние, я взял часовые цены закрытия с 2010-го года для сбера и газа и с 2013-го для EURUSD.

Дополнительно сформировал псевдослучайную выборку такой же длины, как и данные сбера/газпрома.

Результаты:

газпром - 1.2598
сбер - 1.2602
eurusd - 1.1964
рандом - 1.2595
+2
- Маркин Павел
  18 декабря 2016, 22:47
  bstone, В споре рождается истина, поэтому без комментариев невозможно, Лови 10 рандомов, каждый по 800000 битных знаков, попробуй упакуй, ссылка.
  Может у тебя именно псевдо-рандомы? многие реализации языков программирования грешат некачественной реализацией ГПСЧ
  0
  - bstone
    18 декабря 2016, 23:28
    Маркин Павел, нет, в споре рождается тупость вроде моей. Твои сомнения заставили меня перепроверить код и я увидел, что лажанулся в упаковке битового потока. Но… результаты тем не менее, тебя не обрадуют:
    
    сбер - 0.9647
    газпром - 0.9647
    eurusd - 0.9386
    псевдо-рандом (длина сбера) — 0.9648
    псевдо-рандом (длина евро) - 0.9404
    +1
    - bstone
      18 декабря 2016, 23:33
      Ну и для пущей важности взял атмосферные флуктуации с random.org, длина серии соответствует котировкам eurusd. Коэффициент сжатия 0.9403. Так что псевдо-рандом довольно хорош.
      +1
      - Маркин Павел
        18 декабря 2016, 23:52
        bstone, обрадуют, понимаешь когда ты перешёл на битовый знак ты изменил нормальное распределение приращений инструментов на равномерное, чего и рандом взял равномерный. а равномерное распределение = белый шум = несжимаемость.
        А вот если брать рандом с нормальным распределением то ...
        
        В любом случае спасибо за конструктивные идеи.
        0
        bstone
        18 декабря 2016, 23:57
        Маркин Павел, ну смысл в том, что эффективное сжатие должно было бы намекать на наличие повторяющихся паттернов… так вот, если этих паттернов нет в знаках приращений, то их не будет и в последовательности приращений. Очевидно?
        0
        bstone
        19 декабря 2016, 10:46
        Маркин Павел, и все-таки считаю конструктивной идею анализа не коэффициента сжатия как такового, а сравнение его с образцом случайной серии такой же длины. Архиваторы как ни крути работают с байтовым потоком, а не битовым, и это ломает границы потенциальных паттернов.
        0
        Маркин Павел
        19 декабря 2016, 11:20
        bstone, архиваторы уже лет 15-20 работают и с битовым потоком и большими числами (например 16,32,64 байта).
        0
        bstone
        19 декабря 2016, 11:46
        Маркин Павел, специализированные режимы допускаю вполне, попробуйте. Но Huffman, LZ, арифмитическое кодирование и их вариации в архиваторах четко ориентированы на байтовые потоки.
        
        Я, кстати, выдал знаки приращений в байтовый поток, используя три состояния (0, +1, -1), чтобы не было биаса от нулевых приращений. Так вот, коэффициент сжатия получился около 5. Почувствуйте разницу относительно битового потока. Но газпром и сбер сжался даже чуть хуже, чем псевдо-случайная последовательность :)
        0
        Маркин Павел
        19 декабря 2016, 12:07
        bstone, Не скатывайся в поиск мелочей и не зацикливайся.
        
        эффектный и эффективный пример сжатия бесконечного ряда — фракталы — красивая картинка с множеством мандельброта размером 64000х64000 пикселей будет весить ~ 4 гигабайт, а в виде программного кода не более 50 килобайт.
        0
        bstone
        19 декабря 2016, 12:10
        Маркин Павел, не надо путать сжатие с генерацией.
        0
        Маркин Павел
        19 декабря 2016, 12:15
        bstone, как раз не путаю, на этом и основана колмогоровская сложность
        0