09 июля 2016, 23:04
Альтернатива стандартному Болинджеру - Болинджер через линейную регрессию
Добрый вечер.
При одних и тех же периодах — намного информативней и интересней...
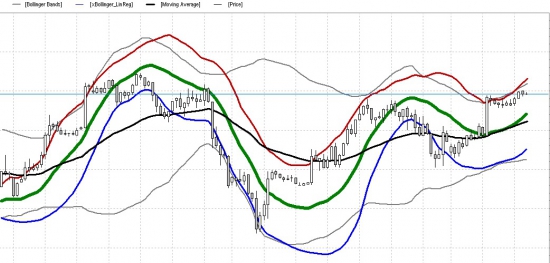
При одних и тех же периодах — намного информативней и интересней...

Settings =
{
Name = "xBollinger_LinReg",
period = 40,
deviation=2,
line=
{
{
Name = "xBollinger_LinReg",
Color = RGB(0, 0, 255),
Type = TYPE_LINE,
Width = 2
},
{
Name = "xBollinger_LinReg",
Color = RGB(192, 0, 0),
Type = TYPE_LINE,
Width = 2
},
{
Name = "xBollinger_LinReg",
Color = RGB(0, 128, 0),
Type = TYPE_LINE,
Width = 6
}
}
}
function c_FF()
local AMA={}
local CC={}
return function(ind, _p,_ddd)
local period = _p
local index = ind
local vol = 0
local sigma = 0
local sigma2 = 0
local aav = 0
local bb = 0
local ZZZ = 0
if index == 1 then
AMA={}
CC={}
CC[index]=(C(index)+H(index)+L(index))/3
AMA[index]=(C(index)+O(index))/2
return nil
end
------------------------------
AMA[index]=AMA[index-1]
CC[index]=(C(index)+H(index)+L(index))/3
if index < (_p) then return nil end
period =_p
if index < period then period = index end
---------------
sigma=0
sigma2=0
aav=0
ZZZ=0
for i = 0, period-1 do
ZZZ=CC[index+i-period+1]
aav=aav+ZZZ
sigma=sigma+ZZZ*(-(period-1)/2+i)
sigma2=sigma2+(-(period-1)/2+i)^2
end
bb=sigma/sigma2
aav=aav/period
AMA[index]=aav+bb*((period-1)/2)
sigma=0
sigma2=0
sigma3 = 0
for i = 0, period-1 do
ZZZ=CC[index+i-period+1]
sigma2=aav+bb*(-(period-1)/2+i)
sigma=sigma+(ZZZ-sigma2)^2
end
sigma=(sigma/period)^(1/2)
return AMA[index]-sigma*_ddd,AMA[index]+sigma*_ddd, AMA[index]
end
end
function Init()
myFF = c_FF()
return 3
end
function OnCalculate(index)
return myFF(index, Settings.period,Settings.deviation)
end
Читайте на SMART-LAB:

Итоги января 2026 — слабое начало года
Данные Росстата по экономической активности за январь и недельной динамике инфляции, по мнению аналитиков «Финама», говорят в пользу продолжения снижения ключевой ставки Банком России на...
17:18
🚀 МТС Банк: про бизнес и портфель
Market Power задал несколько вопросов представителю банка. Публикуем его ответы. ➡️ Отчет компании разобрали здесь ❓ Вопрос МР: Каковы причины снижения непроцентного дохода в 2025 году?...
15:11












Причем тут опережение, когда сам боллинджер самодостаточен и показывает как раз то, что нужно — классическое стдв.