Оптимизация портфеля по минимуму исходных параметров
Для данного метода оптимизации примем некоторые допущения:
- Доходность составляющих портфель финансовых инструментов на будущий период заведомо неизвестна.
- Корреляции финансовых инструментов, входящих в портфель, в будущем не сильно будут отличаться от текущих.
- Волатильности финансовых инструментов пропорциональны общей волатильности рынка, и эти пропорции не будут иметь большого отклонения от текущих значений в будущем периоде.
Для начала рассмотрим самый простой пример.
Пусть у нас есть две акции не коррелирующие между собой (их доходности и движения не зависят друг от друга). В качестве данных для оптимизации возьмем волатильности этих акций, выраженные в виде дисперсий доходности этих акций (доходность и дисперсии рассчитаем из недельных или дневных свечей) D1 и D2.
Необходимо определить веса акций в портфеле W1=?, W2=? При W1+W2=1
Поскольку дисперсии D1 и D2 отражают волатильности акций, то при отсутствии каких-либо других данных и ограничений, целесообразно составить портфель с весами обратно пропорциональными их дисперсий. То есть, чем больше дисперсия у акции, тем меньше ее доля в портфеле.

Простой случай имеет простое решение. В данной ситуации мы не знаем, какая акция будет расти, какая падать и какие вообще будут движения. Но мы оптимизировали свой портфель в расчете на то, что в долгосрочной перспективе рынок склонен к росту.
Теперь возьмем задачу посложнее. Пусть у нас есть две акции с дисперсиями D1 и D2, имеющие между собой зависимость, выраженную ковариацией COV.
Сохраним идею пропорций весов и дисперсий. Но из дисперсий вычтем ковариацию: (D1-COV) и (D2-COV)

Исследуем как зависят веса акций в портфеле от ковариации. Примем, для примера, D1=3, D2=7. Ковариация COV будет переменной Х.
Постоим функции W1=(7-X)/(10-2*X) и W2=(3-X)/(10-2*X).
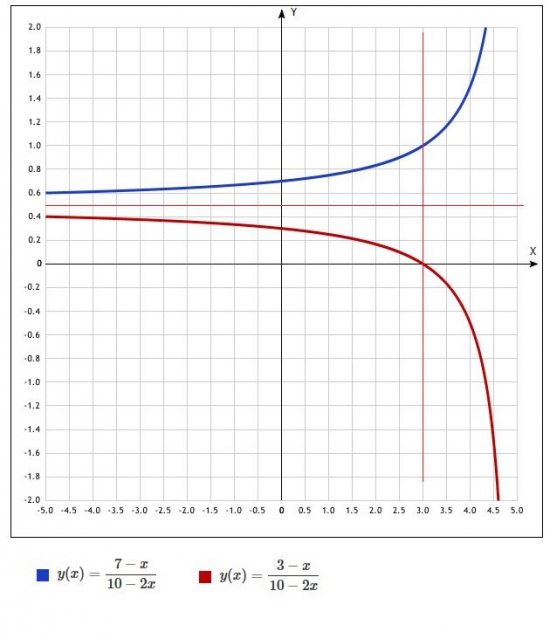
На графике можем видеть, что:
При COV=0 мы получаем веса 0,3 и 0,7.
При COV стремящийся в глубокий минус (корреляция -1) веса стремятся к 0,5/0,5. То есть, когда акции двигаются в противофазе, есть смысл иметь портфель близкий к 0,5/0,5 скорректированный на соотношение дисперсий.
При положительной COV > D1 есть смысл W2 сделать отрицательным (встать в шорт по акции с большей дисперсией, чтобы уменьшить общую дисперсию портфеля).
Выводы: Выше приведенные формулы для расчета портфеля из двух акций, на основании дисперсий и ковариации этих акций, подходят для оптимизации портфеля.
Оптимизация портфеля из большого количества акций
Задача оптимизации портфеля из большого количества акций осложняется тем, что количество параметров сильно увеличивается с количеством рассчитываемых элементов. В большом портфеле необходимо учитывать все возможные корреляции между всеми элементами портфеля. Используя метод пропорций дисперсий, нет возможности построить систему линейных уравнений для большого количества элементов. Поэтому для вычислений будем использовать последовательный метод оптимизации. Общий принцип последовательной оптимизации заключается в том, что мы оптимизируем акции попарно, создавая мини-портфели, которые в дальнейшем попарно оптимизируем с другими мини-портфелями или акциями. То есть, мы производим последовательную попарную оптимизацию, пока не останется один портфель.
Пусть у нас есть 5 акций из которых нужно составить портфель (А1, А2, А3, А4, А5).
Оптимизация начинается с четко определенных условий. Первой парой для оптимизации является пара акций у которой корреляция ближе всего к (-1).
Для начала расчета нам понадобится таблица корреляций
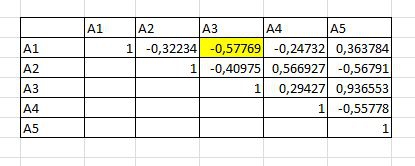
Первой парой будут А1-А3. Проведя расчет мы получим набор для дальнейших расчетов (А1-А3, А2, А4, А5). Теперь нам следует найти корреляцию портфеля А1-А3 относительно остальных элементов и выбрать наименьшее значение для дальнейшего расчета.
Из оставшихся значений корреляции и полученных новых необходимо снова выбрать наименьшее значение, и провести расчеты для следующей пары.
Данный алгоритм применять к массиву полученных портфелей и акций до тех пор, пока всё не свернется в один портфель. Схематично это выглядит так:
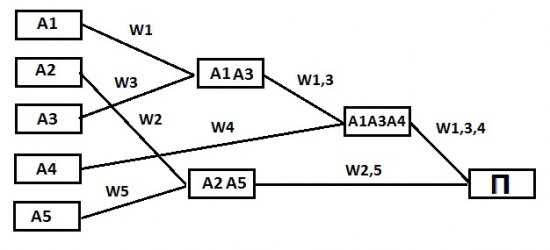
Для нахождения веса акции в общем портфеле необходимо перемножить все веса находящиеся на пути от акции до конечного портфеля:
Wa1 = W1*W1,3*W1,3,4
Wa2 = W2*W2,5
Wa3 = W3*W1,3*W1,3,4
Wa4 = W4*W1,3,4
Wa5 = W5*W2,5
В результате получаем веса акций в искомом оптимизированном портфеле.
На первый взгляд, расчет кажется очень сложным и громоздким, особенно если необходимо будет составить портфель из очень большого количества акций. Но этот способ оптимизации имеет четкий и однозначный алгоритм. Поэтому, он легко автоматизируется. И вся работа по расчету будет сводиться к корректной загрузке данных в программу для оптимизации.
Проверка качества оптимизации и сравнение результатов
Проверка результата проводилась следующим образом:
— проводился расчет портфеля по данному алгоритму;
— на исторических данных определялась дисперсия и доходность портфеля;
— проводился расчет портфеля методом Марковица, где для расчета использовалась доходность портфеля исследуемого метода;
— сравнивались дисперсии разных методов.
Проверка показала что дисперсия для портфеля полученного данным методом на 5-10% меньше, чем дисперсия рассчитанная методом Марковица. То есть риск полученного портфеля меньше на 5-10% при одинаковой доходности.
Такие результаты могут показаться ошибочными. Как может метод итерации быть лучше, чем математическое нахождение оптимальной точки???
Но дело в том, что входные данные (дисперсии и ковариации) при их определении имеют некую погрешность. При использовании метода Марковица (поиск оптимальной точки) любая погрешность уводит нас от оптимального значения. А общая ошибка – сумма векторов ошибок направленных от точки оптимальности. И чем больше используется входных параметров, тем больше суммарная ошибка. Поскольку погрешности присутствуют всегда, то методом Марковица в принципе невозможно точно попасть в оптимальную току.
В нашем способе оптимизации портфеля ошибки арифметически складываются и имеют разный знак, поскольку из дисперсий вычитаются ковариации определяемые таким же методом. В результате общая ошибка будет небольшой, и есть вероятность попадания в оптимальную точку.
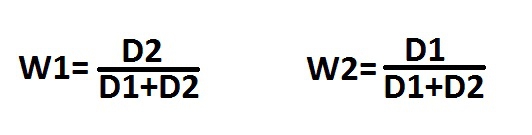










UPD. Рекомендую почитать https://en.wikipedia.org/wiki/Modern_portfolio_theory, потом копать по ссылкам внизу страницы.
Возможно, кто-то такую схему уже описал, но это не столь важно. Может быть кому-то пригодиться эта идея для его работы.
Просто блестяще! Очень сильно.
Такой подход практически не изменил результат.
Я проводил тестирование на истории за 10 лет. И иногда получалось, что портфель из множества активов с одинаковыми весами показывал результат лучше, чем самый хитровыдуманный портфель. :)
Для себя я сделал методику расчета, которую буду использовать сам и передам свои потомкам. Она немного упрощенная, но вполне годится для пользователя не сильно продвинутого в математике.
FZF, портфель с равными весами иногда выигрывает у других методик, иногда проигрывает. Результат в основном случайный и зависит от конкретных событий и процессов, которые будут происходить с эмитентами, товарами, валютами. Поскольку мы почти ничерта не знаем про будущее, то и портфельные теории представляют собой жалкое зрелище.
Меня заинтересовала другая мысль. Вы использовали дисперсию доходностей акций. Но в свете недавних событий с отрицательными ценами использование доходностей (или приращений логарифмов цен) в эконометрике поставлено под огромное сомнение и скорее всего должно быть отвергнуто. Может, действительно эффективней работать с арифметическими разностями цен и анализировать именно их дисперсию без предварительного логарифмирования?..
FZF, =) видимо, надо просто пробовать.
С точки зрения долгосрочного инвестирования (более 10 лет) доминирующим фактором как раз будет правильно определение предсказание знака будущей среднегодовой доходности инструментов в портфеле.
А для предлагаемой Вами методики кажется разумным использовать как можно более короткие периоды ребалансировки, чтобы подавить влияние долгосрочного среднего. Допустим, взять фьючерс MM и фьючерс Si. Их ковариация по идее отрицательная. Можно из них составить разумный портфель и ребалансировать его ежедневно в 18:40 или 19:05? Или в 11:00? Что получится из такого замеса?
FZF, волатильность фьючерса СИ сейчас 10% годовых, волатильность фьючерса Сбера 20% годовых.
Дисперсия соответственно 0.01 и 0.04. Получается отношение дисперсий 1-к-4. То есть 80% денег надо грузить во фьючерс СИ и 20% грузить во фьючерс Сбера?
Сейчас фьючерс SR ~ 23 000; фьючерс СИ ~ 75 000.
1 миллион рублей даёт портфель 10.6666(6) лота Si в паре с 8.696 лотов SR?
FZF, задача портфеля — уменьшить просадку.
Кстати, задумался о том, как посчитать ковариацию. Между чем и чем её надо измерять? Построил точечный график рассеяния для цен SiU0(SRU0) и получил положительную ковариацию. Но, очевидно, это просто за счет того, что «сбер всегда растет» и «доллар всегда растет».![]()