Ценная подборка №29. Риски и плечи.

Что будет происходить со счетом, если в известной последовательности сделок мы используем плечо. Ответ оказался не так прост. И зависит от нашей стратегии.
Пусть r1, r2,…rN – доходности сделок 1,2…N. Если мы не используем рефинансирование (т.е. торгуем всегда только на начальную сумму счета), то ответ достаточно прост. Общая доходность равна сумме доходностей D=r1+r2+…rN и применение плеча K в каждой сделке приводит к изменению результата в К раз, при условии, что в последовательности не встретится сделки, которая обнулит счет.
 
Т.е. если все ri*K>-1, то результат равен K*D=K*( r1+r2+…rN).
 
Ситуация становится гораздо интереснее, если мы используем рефинансирование, т.е. используем заработанное для входа в новую сделку (или всегда торгуем на всю сумму счета). В этом случае доходность результата последовательности сделок задается формулой: D=(1+r1)*(1+r2)*…*(1+rN)-1. Применение плеча K приводит к следующей формуле

D=(1+K*r1)*(1+K*r2)*…*(1+K*rN)-1.
 
В этом случае итоговый результат начинает сложным (нелинейным) образом зависеть от размера плеча К.
 
Попробуем разобраться с простейшим случаем последовательности из двух сделок. Общая доходность последовательности из двух сделок, совершенных с плечом К и использованием рефинансирования будет равна:
 
D=(1+K*r1)*(1+K*r2) -1=1+K*r1+K*r2+K*K*r1*r2-1=K*(r1+r2)+K*K*r1*r2.
 
Доходность получается сложной нелинейной функцией трех переменных – двух доходностей и плеча. Представить итоговый результат в графической форме достаточно сложно, однако можно провести исследования того какой результат в каждой из сделкок даст нам положительный результат по итогу при заданном уровне плеча.
 
Сначала найдем функцию, задающую наборы результатов в каждой сделке, такие, что итоговый результат равен нулю при заданной величине плеча К. Для этого надо приравнять D к нулю и выразить r2 через К и r1.
 
K*(r1+r2)+K*K*r1*r2=0
 
r2=-r1/(1+K*r2)=F(K,r1)
 
Если мы представим себе плоскость на которой ось Х задает доходность первой сделки r1, а ось Y задает доходность второй сделки r2, то функция F(K,r1) задает множество пар r1 и r2, таких, что итоговая доходность двух сделок равна нулю. Такие функции еще называют сепаратрисами. Помните из школы «биссектриса – это такая крыса, которая бегает по углам и делит угол пополам». Так вот сепаратриса – это такая крыса, которая бегает по плоскостям и делит плоскость на две части:  справа от нее общий результат двух сделок положителен, а слева от нее результат последовательности двух сделок отрицателен. :)
 
Это нарисовано на графике:




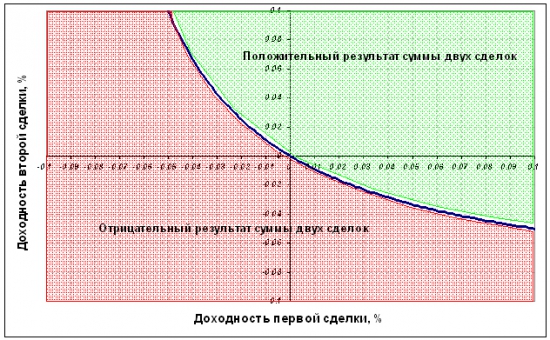
Здесь синяя линия – сепаратриса для значения плеча К=5. Зеленая область – все наборы доходностей при которых общий результат в двух сделках будет положительным, а красная область все наборы доходностей, при которых общий результат в двух сделках будет отрицательным. Уже здесь видно, что при плече К=5 область при которой общий результат будет положительным меньше, чем область возможных отрицательных результатов.
 
То же происходит при увеличении плеча? Построим на одном графике сеператрисы для значений плеча, равных 1, 2, 5, 10 и 20:
 



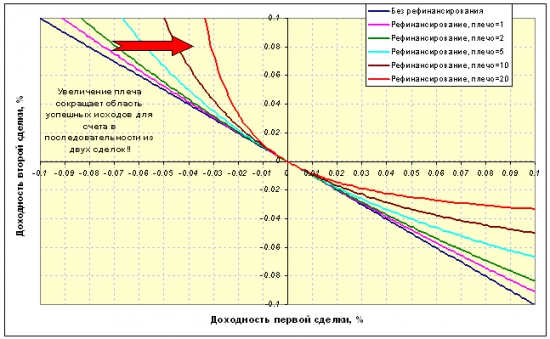
Очень хорошо видно, что увеличение плеча уменьшает область возможных положительных исходов для счета в последовательности их двух сделок. При плече К=20, даже поймав в первой сделке рост на 10 %, мы можем второй сделкой, в которой результат будет всего -4 %, уйти в итоге в минус.
 
А что же в последовательности из N сделок? (Тем, кто прочитал до этого места и уже отплевывается от пережеванных формул, следует сразу переходить к выводу).

В последовательности из N сделок сепаратриссой будет сложная эн-минус-один-мерная поверхность в эн-мерном пространстве, но общий вывод останется неизменным, только вероятность положительного исхода при увеличении плеча будет сокращаться гораздо быстрее, чем в последовательности из двух сделок.

Применение плеча при торговле с реинвестированием резко сокращает вероятность положительного исхода для счета в целом.


Автор: Mikola

А так же ценные подборки с 1 по 28