28 июня 2015, 17:42
Quantitative trading for dummies. Part 2 (Корреляция коинтеграция)
Добрый день! Перед вами вторая часть цикла статей Quantitative trading for dummies. Сегодня поговорим о корреляции и коинтеграции. И так, я снова постараюсь обьяснить все максимально доступно и без страшных формул.
В качестве примера для объяснения я возьму часто приводимый жизненный пример «Пьяницы и собака».
Представьте себе что два алконавта идут по улице, движение алконавтов случайно. Это можно изобразить следующим образом.
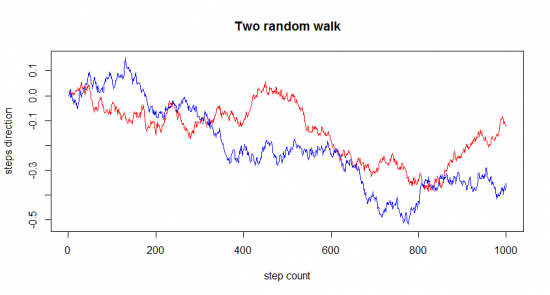
Теперь представим что на сторонах улицы находятся бары, и каждый алконавт услышав рекламу бара шагает в его сторону с определенной вероятностью. О таких временных последовательностях говорят что они коррелированны. На графике это можно представить следующим образом.
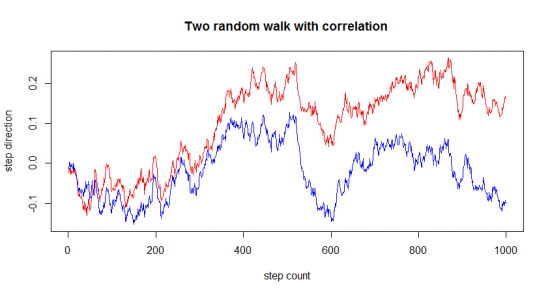
Представьте, что один из алконавтов идет с собакой на поводке, движение алконавта по прежнему случайно, но вот движение собаки ограничено поводком ( тут кстати можно поспорить, чье движение случайно, а чье ограничено поводком). Несмотря на то что по отдельности кривые очень напоминают случайно блуждание они никогда не расходятся на расстояние большее чем поводок, и всякий раз, после разбредания в разные стороны, они снова стремятся друг другу, так как величина поводка ограничена. О таких временных последовательностях говорят, что они коинтегрированы. Коинтеграция является гораздо более важным понятием в теории временных рядов, чем корреляция.
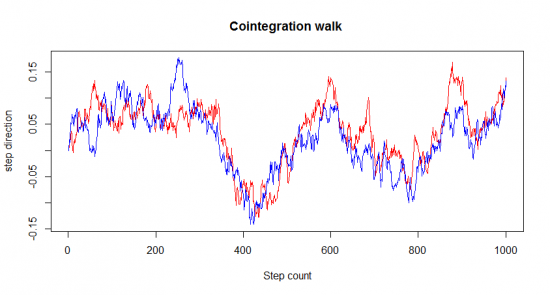
Теперь вернемся к финансам. Представьте что вы нашли две акции движение цен которых сильно коррелировано друг с другом, значит ли это что если их движение сильно разошлось то можно продать дорогую бумагу и купить дешевую (продать спред). Нет не значит! Цена может не сойтись никогда! Совершенно другое дело когда два ряда коинтегрированны, если в какой-то момент времени их цены разошлись то мы можем продать дорогую и купить дешевую. Только вот вопрос, как найти такой ряд.
Коинтеграция
Прежде всего, стоит все-таки определить, что такое коинтеграция. Существует точное математическое определение коинтеграции:
Что такое стационарный временной ряд? Если совсем просто, то это временной ряд свойства которого не меняются во времени. Т.е. если мы возьмем некий его отрезок, посчитаем стандартные статистические характеристики, такие как математическое ожидание или дисперсию, мы должны получить одинаковые величины, в пределах погрешности, естественно. Пример чистого стационарного ряда это к примеру случайное блуждание, либо синусойда.
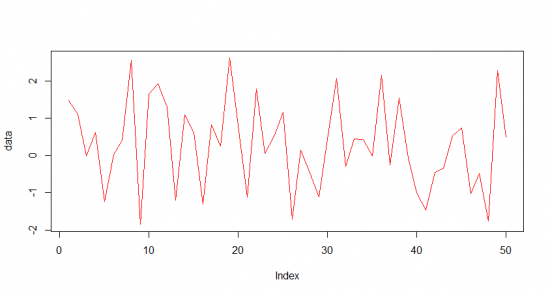
Стационарный временной ряд имеет порядок интегрирования 0. Обратное не верно. Возьмем теперь стационарный ряд X1, X2… Xn, и преобразуем его в следующий ряд: Y1 = X1, Y2 = Y1 + X2,… Yn = Yn-1 + Xn получившийся ряд имеет порядок интегрирования 1. Если вернуться к определению, то временной ряд имеет порядок интегрирования 1 если ряд его приращений имеет порядок интегрирования 0. Аналогично можно определить более высокие порядки интегрирования. Рассмотрим пример ряда, интегрированого с порядком 1:
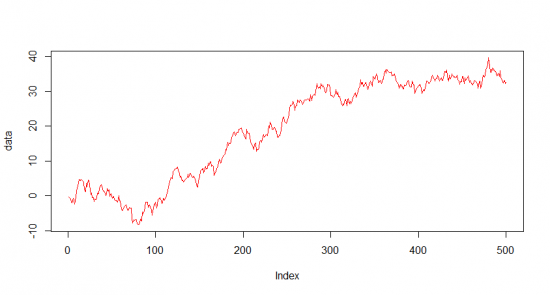
Сумма случайных блужданий является примером такого ряда. Теперь мы можем переформулировать определение коинтеграции в применении для цен.
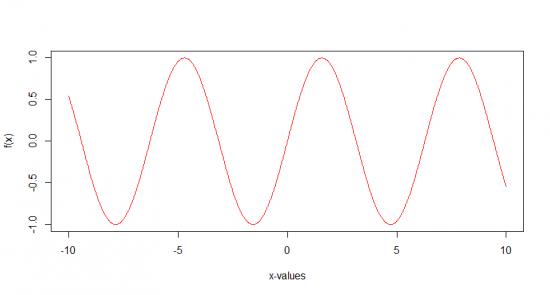
В таком случае вам конечно же не придется проверять ряд на стационарность, по графику и так все видно.
Перейдем к практике
В реальной жизни вы конечно же не получите спред похожий на синусойду. Возьмем цены двух компаний, пусть будут TATN и TATNP. Посчитаем спред и проверим полученный ряд на стационарость, что бы понять, являются ли наши ряды (TATN, TATNP) коинтегрированны. И если это так, то мы можем торговать статистический арбитраж. И так, для начала построим отношение цен акции TATN к TATNP, спред можно строить так же вычитая TATN- TATN * hadge coeficent. Что такое hadge coeficent это коэффициент b полученный из линейной регрессии, вы можете прочесть об этом в первой части. И так, строим спред!
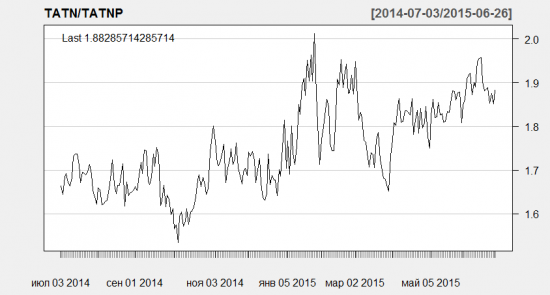
И так, мы видим на глаз что спред все же похож на стационарный ряд, давайте проверим это! Для этого существует тест Тест Дики-Фуллера это далеко не единственный тест на стационарность, но в данном примере мы используем именного его. Результат:
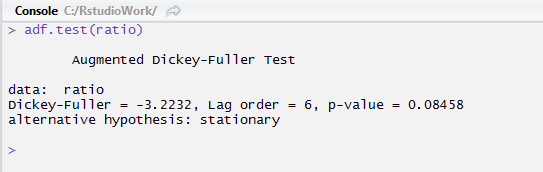
Видим, что. p-value мал, и отсюда можем утверждать, что действительно TATN и TATNP коинтегрированны. Что подтверждается визуально на графике:
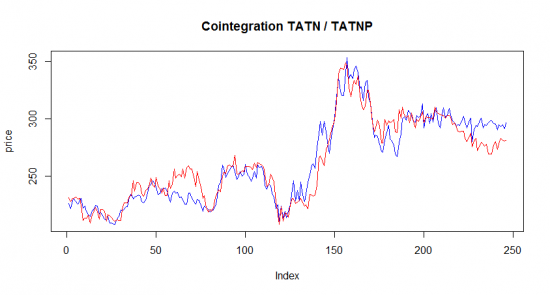
Обратите внимание на строку в коде TATNP$TATNP.Close*coef(model)[2]+coef(model)[1]. В первой часте я писал что линейная регрессия потребуется в парном трейдинге. Можно ее переписать так.
Заключение: И так, мы разобрались что же такое корреляция и коинтеграция, и убедились что ряд цен акции TATN и TATNP коинтегрированны, а следовательно годятся для торговли стратегии статический арбитраж. Теперь вы можете строить свои арбитражные стратегии опираясь на полученный опыт. Не стоит сбрасывать со счетов корреляцию, опираясь на этот эффект существует целый пласт импульсных стратегий, об этом поговорим в других частях.
В качестве примера для объяснения я возьму часто приводимый жизненный пример «Пьяницы и собака».
Представьте себе что два алконавта идут по улице, движение алконавтов случайно. Это можно изобразить следующим образом.

Теперь представим что на сторонах улицы находятся бары, и каждый алконавт услышав рекламу бара шагает в его сторону с определенной вероятностью. О таких временных последовательностях говорят что они коррелированны. На графике это можно представить следующим образом.

Представьте, что один из алконавтов идет с собакой на поводке, движение алконавта по прежнему случайно, но вот движение собаки ограничено поводком ( тут кстати можно поспорить, чье движение случайно, а чье ограничено поводком). Несмотря на то что по отдельности кривые очень напоминают случайно блуждание они никогда не расходятся на расстояние большее чем поводок, и всякий раз, после разбредания в разные стороны, они снова стремятся друг другу, так как величина поводка ограничена. О таких временных последовательностях говорят, что они коинтегрированы. Коинтеграция является гораздо более важным понятием в теории временных рядов, чем корреляция.

Теперь вернемся к финансам. Представьте что вы нашли две акции движение цен которых сильно коррелировано друг с другом, значит ли это что если их движение сильно разошлось то можно продать дорогую бумагу и купить дешевую (продать спред). Нет не значит! Цена может не сойтись никогда! Совершенно другое дело когда два ряда коинтегрированны, если в какой-то момент времени их цены разошлись то мы можем продать дорогую и купить дешевую. Только вот вопрос, как найти такой ряд.
Коинтеграция
Прежде всего, стоит все-таки определить, что такое коинтеграция. Существует точное математическое определение коинтеграции:
- Если некоторая линейная комбинация двух временных рядов имеет порядок интегрирования меньший чем порядок интегрирования каждого из рядов, то говорят, что временные ряды коинтегрированы.
Что такое стационарный временной ряд? Если совсем просто, то это временной ряд свойства которого не меняются во времени. Т.е. если мы возьмем некий его отрезок, посчитаем стандартные статистические характеристики, такие как математическое ожидание или дисперсию, мы должны получить одинаковые величины, в пределах погрешности, естественно. Пример чистого стационарного ряда это к примеру случайное блуждание, либо синусойда.
data <- rnorm(50) plot(data, type='l', col='red')

Стационарный временной ряд имеет порядок интегрирования 0. Обратное не верно. Возьмем теперь стационарный ряд X1, X2… Xn, и преобразуем его в следующий ряд: Y1 = X1, Y2 = Y1 + X2,… Yn = Yn-1 + Xn получившийся ряд имеет порядок интегрирования 1. Если вернуться к определению, то временной ряд имеет порядок интегрирования 1 если ряд его приращений имеет порядок интегрирования 0. Аналогично можно определить более высокие порядки интегрирования. Рассмотрим пример ряда, интегрированого с порядком 1:
data <- cumsum(rnorm(500)) plot(data, type='l',col="red")

Сумма случайных блужданий является примером такого ряда. Теперь мы можем переформулировать определение коинтеграции в применении для цен.
- Два временных ряда цен коинтегрированны если мы можем найти такую их линейную комбинацию, которая является стационарным временным рядом.

В таком случае вам конечно же не придется проверять ряд на стационарность, по графику и так все видно.
Перейдем к практике
В реальной жизни вы конечно же не получите спред похожий на синусойду. Возьмем цены двух компаний, пусть будут TATN и TATNP. Посчитаем спред и проверим полученный ряд на стационарость, что бы понять, являются ли наши ряды (TATN, TATNP) коинтегрированны. И если это так, то мы можем торговать статистический арбитраж. И так, для начала построим отношение цен акции TATN к TATNP, спред можно строить так же вычитая TATN- TATN * hadge coeficent. Что такое hadge coeficent это коэффициент b полученный из линейной регрессии, вы можете прочесть об этом в первой части. И так, строим спред!
getSymbols("TATN", from=Sys.Date()-360, src="Finam", period='day')
getSymbols("TATNP", from=Sys.Date()-360, src="Finam", period='day')
data <- cbind(Cl(TATN),Cl(TATNP))
data <- data[complete.cases(data)]
ratio <- c(data[,1]/data[,2])
chartSeries(ratio, theme = chartTheme("white", up.col='black'), name = 'TATN/TATNP')

И так, мы видим на глаз что спред все же похож на стационарный ряд, давайте проверим это! Для этого существует тест Тест Дики-Фуллера это далеко не единственный тест на стационарность, но в данном примере мы используем именного его. Результат:

Видим, что. p-value мал, и отсюда можем утверждать, что действительно TATN и TATNP коинтегрированны. Что подтверждается визуально на графике:
plot(as.vector(TATN$TATN.Close), col='blue', type='l', main='Cointegration TATN и TATNP', ylab='price') lines(as.vector(TATNP$TATNP.Close*coef(model)[2]+coef(model)[1]), col='red', type='l')

Обратите внимание на строку в коде TATNP$TATNP.Close*coef(model)[2]+coef(model)[1]. В первой часте я писал что линейная регрессия потребуется в парном трейдинге. Можно ее переписать так.
TATN$TATN.Close = TATNP$TATNP.Close*coef(model)[2]+coef(model)[1].Это линейное уравнение, линейной регрессии из первой части, где coef(model)[2] — Коэффициент b, а coef(model)[1] — коэффициент a, а сам спред по сути является остатками (Residuals). Обо всем это я писал в предыдущей части!
Заключение: И так, мы разобрались что же такое корреляция и коинтеграция, и убедились что ряд цен акции TATN и TATNP коинтегрированны, а следовательно годятся для торговли стратегии статический арбитраж. Теперь вы можете строить свои арбитражные стратегии опираясь на полученный опыт. Не стоит сбрасывать со счетов корреляцию, опираясь на этот эффект существует целый пласт импульсных стратегий, об этом поговорим в других частях.
Читайте на SMART-LAB:

Режим risk-off: почему удар по Ирану усилил доллар, но не поддержал облигации
Понедельник начался с довольного нетипичного режима риск-офф: доллар укрепляется по всему рынку, мировые акции снижаются, золото выросло более чем на 4%, Brent в моменте подскакивал на 13%....
02.03.2026
Открыли 1 000-й магазин КООП ОКОЛО в Татарстане
Юбилейный магазин «КООП ОКОЛО», площадью 240 кв. м открылся в селе Дубъязы Республики Татарстан. В нем представлено более 6 000 товаров, среди которых продукция собственного производства...
02.03.2026












А вообще не рекомендую торговать парный трейдинг категорически. При тех-же результатах, если не хуже — вы платите удвоенные комиссии и прочие издержки.
Правда, бывают шпильки, но без робота их поймать нереально.