Can you solve this puzzle? (Задача)

 

Source link: http://www.optiver.com/amsterdam/careers/job-vacancies/details/5341/Junior-Researcher


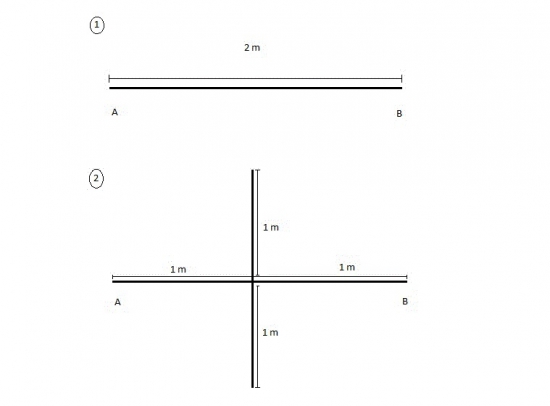
You have to walk from point A to point B 10 times, blindfolded. Every time before you start walking, a fair coin is tossed, and if it comes out heads, a wall in the middle is present (situation 2 in the picture), while if it comes out tails it is not (situation 1 in the picture). As you are blindfolded, you do not know if the wall is present or not.
Even though you are blindfolded, you can move in perfectly straight lines towards any point you choose. Can you give a prescription how to walk from A to B so that the total distance you cover is as small as possible? What distance do you expect to cover in those 10 walks?








Fair Play — in play! Search in Web — is not a solve! ;)
Know this already — don't put an answer.
Solution paths describe — Your bonus points!



Special thanks to Тот самый Артур 





Далее — решите задачку, и только потом — сравнивайте!







Мои рассуждения:
 
Так как задачка для программеров, то решение в виде алгоритма:


1) шагаем от А до центра;
2) чекаем, презент ли уолл;
— иф презент,
3а) муваем ап то 1метр,
4а) зэн муваем стрэйт в точку В
— иф уолл нот презент,
3б) муваем сразу стрэйт в точку В
Усё! ;)
Correct Me if I wrong))))

 


 
Теперь дистанс'ы.

При идеальном раскладе — 10 из 10 — путь равен 20 метрам.
При очень плохом раскладе — 0 из 10 — максимальный путь по алгоритму = 1+1+1.41 = 3.41 х 10 = 34.14 м.

При средней «везучести» — 4 из 10 — путь = (4 х 2м) + (6 х (1+1+1.41м)) = 8 + 20,48 = 28,48 м.
Итого: средняя везучесть «выгрызает» неплохо — восемь с половиной метров из четырнадцати!


Можно было, конечно, ломиться сразу напрямик к верхней (или нижней) точке стены, а затем как в 4а),  но тогда полный путь будет = 2 х 1.414 х 10 = 28.28 м.
Таким образом, обыгрываем dumb_throught даже при трёх «не_стенах.» Алгоритм признаём живучим.))

Ответ на второй вопрос: «No greater than 31 meters.»





Интересно — меня бы взяли?))))