13 июня 2021, 02:04
Интересный эффект в портфельном инвестировании
Недавно для себя открыл интересное явление в портфельном инвестировании
Оно заключается в том что количество акций в портфеле с прибылью меняется по линейному закону в то время как сама прибыль меняется по квадратичному (по параболе — растет быстрее)
Рассмотрим на примере
Если мы возьмем распределение прибыли и убытков в портфеле и попробуем рассчитать общую сумму прибыли и общую сумму убытков и получить их соотношение, а так же соотношение количества акций с отрицательной прибылью и положительной и взять их соотношение, то увидим что, к примеру, для соотношения по количеству 1/3, убыток к прибыли будут соотносится как 1/9 или примерно 0,1.
Другими словами, если мы захотим полностью закрыть портфель фиксируя 10% убытка, забирая 90% прибыли, мы будем избавлять от 25% убыточных акций и 75% прибыльных (90% прибыли создает 3/4 акций, 10% убытка создает 1/3 акций)
А при соотношении в портфеле количества убыточных акций к прибыльным = 1/10, получим всего 1% суммы убытка по отношению к 99% прибыли
Так что не страшно если есть в портфеле убыточные акции и нужно полностью закрывать портфель, можно их закрывать вместе с остальными.
Общий вывод такой: если у вас в портфеле соотношение акций с убыточными позициями и акций с прибыльными позициями = 1/3, то соотношение абсолютных убытков к абсолютной прибыли будет 1/9 = 1^2/3^2 (1/3 возведенная в квадрат). Для выполнения такого условия нужно чтоб каждая акция портфеля покупались на одинаковую величину капитала и чтоб портфель какое-то время после этих покупок был неизменным. Чем дольше портфель не изменен, тем больше он будет соответствовать статистической зависимости. Для других соотношений выполняется то же правило возведения в квадрат.
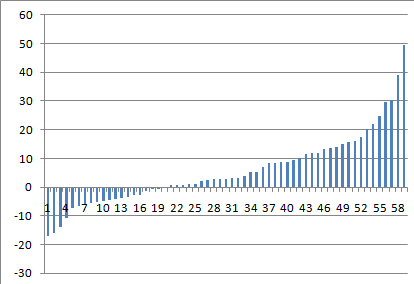
пример реального распределения прибылей
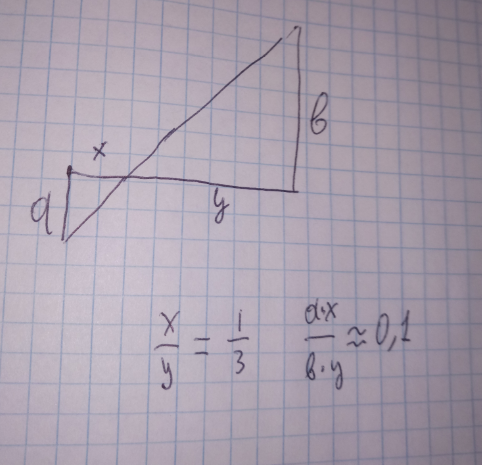
схема расчета (вогнутые стороны треугольника заменил прямыми, т.к. думаю, что это на результат сильно не скажется)
Оно заключается в том что количество акций в портфеле с прибылью меняется по линейному закону в то время как сама прибыль меняется по квадратичному (по параболе — растет быстрее)
Рассмотрим на примере
Если мы возьмем распределение прибыли и убытков в портфеле и попробуем рассчитать общую сумму прибыли и общую сумму убытков и получить их соотношение, а так же соотношение количества акций с отрицательной прибылью и положительной и взять их соотношение, то увидим что, к примеру, для соотношения по количеству 1/3, убыток к прибыли будут соотносится как 1/9 или примерно 0,1.
Другими словами, если мы захотим полностью закрыть портфель фиксируя 10% убытка, забирая 90% прибыли, мы будем избавлять от 25% убыточных акций и 75% прибыльных (90% прибыли создает 3/4 акций, 10% убытка создает 1/3 акций)
А при соотношении в портфеле количества убыточных акций к прибыльным = 1/10, получим всего 1% суммы убытка по отношению к 99% прибыли
Так что не страшно если есть в портфеле убыточные акции и нужно полностью закрывать портфель, можно их закрывать вместе с остальными.
Общий вывод такой: если у вас в портфеле соотношение акций с убыточными позициями и акций с прибыльными позициями = 1/3, то соотношение абсолютных убытков к абсолютной прибыли будет 1/9 = 1^2/3^2 (1/3 возведенная в квадрат). Для выполнения такого условия нужно чтоб каждая акция портфеля покупались на одинаковую величину капитала и чтоб портфель какое-то время после этих покупок был неизменным. Чем дольше портфель не изменен, тем больше он будет соответствовать статистической зависимости. Для других соотношений выполняется то же правило возведения в квадрат.

пример реального распределения прибылей
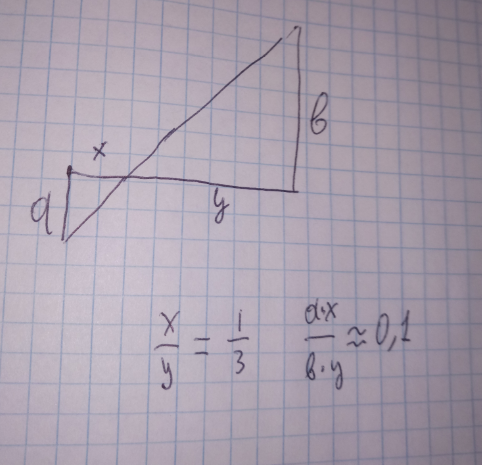
схема расчета (вогнутые стороны треугольника заменил прямыми, т.к. думаю, что это на результат сильно не скажется)
Читайте на SMART-LAB:

Аренадата чудом выполнила гайденс. Сравнение с сектором по мультипликаторам. Прогноз результатов и дивидендов за 2025 год.
Вчера Аренадата опубликовала пресс-релиз . За 2 дня после выхода новостей акции росли максимально до +28%.
Фокус пресс-релиза не на результате, а на том, что компания выполнила гайденс. Сам...
17:36

USD/JPY: в фокусе — борьба за ключевую область
Валютная пара подходит к важной точке пересечения нескольких технических линий: пробитого недельного пологого даунтренда (построенного по максимумам 10.07.2024 и 10.01.2025), уровня поддержки...
20:14












Если ваша ТС прибыльная, то её результаты будут выглядеть как на первом рисунке. Видим, что отношение средней прибыльной сделки к средней убыточной около всеми любимого 3:1. Недостижимо лишь такое отношение количества прибыльных к количеству убыточных (при этом). 1:1 возможно, но 3:1 — вряд ли. Иначе был бы просто золотой дождь.