16 января 2021, 21:01
Совершенствуем Exponential Moving Average (EMA). 2
В топике Совершенствуем Exponential Moving Average (EMA) мы показали использование линейной и нелинейной обратных связей в применении к ЕМА. Как правильно отметили в части комментариев, в случае линейной обратной связи ЕМА просто превращается в другую ЕМА с меньшим периодом, и толку от такой ЕМА немного. И тем не менее, даже в этом случае, обратная связь демонстрирует то, что и должна была демонстрировать — цель достигнута и ошибка слежения за ценой уменьшилась.
Нелинейная же связь даже в случае с ЕМА работает нормально, и по факту адаптивно в зависимости от ошибки меняет период сглаживания. При больших значениях ошибки период сглаживания уменьшается относительно заданного Тс, при малых ошибках период сглаживания практически равен предустановленному Тс.
В общем, нам надо решить вопрос только с линейной обратной связи, и выбрать для этого в качестве исходного индикатора что-то посложнее ЕМА. Скажем фильтр низких частот (ФНЧ) 2-го порядка. Выражение для него будет иметь вид.
Y(t) = a0*X(t) + b1*Y(t-1) + b2*Y(t-2)
Немногим сложнее обычной ЕМА, ничего ужасного.)
Попробуем такой фильтр сделать из обычной ЕМА вида Y(t) = a0*X(t) +b1*Y(t-1) пропустив сигнал вначале через оду ЕМА, а затем через вторую. Вот так: Y(t) =EMA(EМА(X(t)).
То, что мы сделаем сейчас не совсем обычно с точки зрения алгебры, но, тем не менее, результат от этого не пострадает. Перемножим преобразованные выражения двух одинаковых ЕМА друг на друга, чтобы получить более сложную ЕМА. Вообще-то, это называется z-преобразование.
Н(z) =(a0/(1-b*1z^-1)*(a0/(1-b1*z^-1)
Н(z) = a0^2/(1 -b1*z^-1 — b1*z^-1 + b1^2*(z^-1)^2) или
Н(z) = a0^2/(1 -2*b1*z^-1 + b1^2*z^-2).
А теперь вернувшись из этой абракадабры к обычному виду записи индикаторов, получим:
Y(t) = a0^2*X(t) + 2*b1*Y(t-1) — b1^2*Y(t-2),
где a0 и b1 коэффициенты нашей исходной ЕМА.
и это будет тоже самое, как если бы мы 2 раза пропустили X(t) через ЕМА. График такой ЕМА 2-го порядка ЕМА2 на единичном скачке будет выглядеть примерно так:
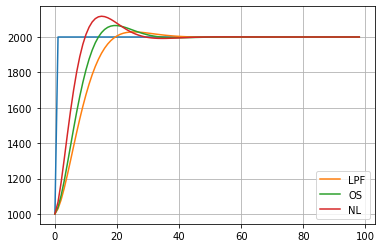
Смотри график LPF, в том числе и в предыдущем топике.
На таком фильтре ЕМА2 уже есть где разгуляться и с линейными, и с нелинейными обратными связями, и еще много с чем другим.)
Об этом мы, возможно, в следующий раз поговорим. Если будет с кем.)
Кто хочет продолжения темы — голосуйте, в смысле, ставьте плюсы. Я не буду тратить время и писать в пустоту. Извините за каламбур.)
Удачи!
Нелинейная же связь даже в случае с ЕМА работает нормально, и по факту адаптивно в зависимости от ошибки меняет период сглаживания. При больших значениях ошибки период сглаживания уменьшается относительно заданного Тс, при малых ошибках период сглаживания практически равен предустановленному Тс.
В общем, нам надо решить вопрос только с линейной обратной связи, и выбрать для этого в качестве исходного индикатора что-то посложнее ЕМА. Скажем фильтр низких частот (ФНЧ) 2-го порядка. Выражение для него будет иметь вид.
Y(t) = a0*X(t) + b1*Y(t-1) + b2*Y(t-2)
Немногим сложнее обычной ЕМА, ничего ужасного.)
Попробуем такой фильтр сделать из обычной ЕМА вида Y(t) = a0*X(t) +b1*Y(t-1) пропустив сигнал вначале через оду ЕМА, а затем через вторую. Вот так: Y(t) =EMA(EМА(X(t)).
То, что мы сделаем сейчас не совсем обычно с точки зрения алгебры, но, тем не менее, результат от этого не пострадает. Перемножим преобразованные выражения двух одинаковых ЕМА друг на друга, чтобы получить более сложную ЕМА. Вообще-то, это называется z-преобразование.
Н(z) =(a0/(1-b*1z^-1)*(a0/(1-b1*z^-1)
Н(z) = a0^2/(1 -b1*z^-1 — b1*z^-1 + b1^2*(z^-1)^2) или
Н(z) = a0^2/(1 -2*b1*z^-1 + b1^2*z^-2).
А теперь вернувшись из этой абракадабры к обычному виду записи индикаторов, получим:
Y(t) = a0^2*X(t) + 2*b1*Y(t-1) — b1^2*Y(t-2),
где a0 и b1 коэффициенты нашей исходной ЕМА.
и это будет тоже самое, как если бы мы 2 раза пропустили X(t) через ЕМА. График такой ЕМА 2-го порядка ЕМА2 на единичном скачке будет выглядеть примерно так:

Смотри график LPF, в том числе и в предыдущем топике.
На таком фильтре ЕМА2 уже есть где разгуляться и с линейными, и с нелинейными обратными связями, и еще много с чем другим.)
Об этом мы, возможно, в следующий раз поговорим. Если будет с кем.)
Кто хочет продолжения темы — голосуйте, в смысле, ставьте плюсы. Я не буду тратить время и писать в пустоту. Извините за каламбур.)
Удачи!
15 Комментариев
 GoGo16 января 2021, 21:47Смысл функции сглаживания, как это ни странно, сгладить. То есть, грубо говоря, выдать нечто среднее. Как с её помощью предвидеть дальнейшее движение непонятно?+1
GoGo16 января 2021, 21:47Смысл функции сглаживания, как это ни странно, сгладить. То есть, грубо говоря, выдать нечто среднее. Как с её помощью предвидеть дальнейшее движение непонятно?+1 asfa16 января 2021, 21:50Также получается DEMA ??0
asfa16 января 2021, 21:50Также получается DEMA ??0
Читайте на SMART-LAB:

NAT.GAS: Газовый арбитраж на пороге взрыва — зажжет ли Европа американский хаб?
На европейских рынках котировки на природный газ (TTF) сегодня взлетели на 45%, превысив отметку €46/МВт·ч ($570 за 1000 м³). Европа критически зависит от танкеров из Катара, которые сейчас...
02.03.2026

Павел Крутолапов назначен генеральным директором ПАО "АПРИ"
Павел Крутолапов назначен генеральным директором ПАО «АПРИ»
С 2023 года Павел занимал должность главного архитектора ПАО «АПРИ» и отвечал за продуктовое направление компании,...
02.03.2026










