27 сентября 2020, 21:25
Как заработать на случайном блуждании. Часть 9.
М-да...
И все ж таки — какой же на рынке процесс? Случайный али нет? Есть ли хотя бы надежда припасть к Граалю и напиться из него Счастия?
Собственно говоря, неважно — какое именно уравнение описывает динамику рынка:
марковское
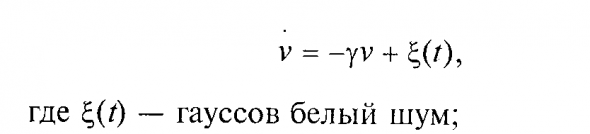
или немарковское:
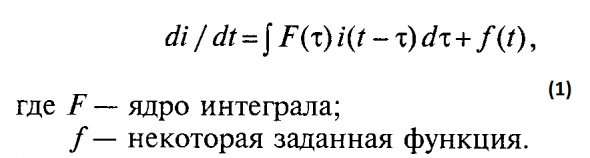
все равно — в правой части этих уравнений к некой прямой линии (сносу, дрифту,...) или скользящей средней всегда прибавляется случайная компонента, интеграл которой образует т.н. «случайное блуждание» и бороться с которым чрезвычайно трудно.
Именно поэтому, абсолютное большинство трейдеров пытаются наполнить карманы наличными, работая «по тренду», т.е. учитывать дрифт цены, либо взирая на поведение SMA, к примеру. А на случайную компоненту стараются не обращать внимания. Хе-хе… Как будто это так просто...
«Постойте!» — возопит особо внимательный страждущий.
«Как же это вы говорите, что для немарковского представления рынка, f(t) — случайная функция, а черным по белому написано, что f(t) — некоторая заданная функция!»
К сожалению — нет. На рынке f(t) — это именно случайная функция, дисперсия которой удовлетворяет зависимости Sigma*sqrt(T), свойственной именно полностью случайным процессам.
Рассмотрим, например, распределение приращений пары AUDUSD за 21 сентября 2020 г. Я даже приводить его гистограмму не буду — оно и так всем известно: островершинное и толстохвостое. Работать будем с архивом котировок от Dukascopy.
1) При анализе цен CLOSE 1-секундных (1S) баров имеем за сутки 34649 таких значений. СКО приращений BID = 0.0000275. СКО приращений ASK = 0.0000306
2) При анализе цен CLOSE 2-секундных (2S) баров имеем за сутки 24694 таких значений. СКО приращений BID = 0.0000325. СКО приращений ASK = 0.0000363
3) При анализе цен CLOSE 3-секундных (3S) баров имеем за сутки 19488 таких значений. СКО приращений BID = 0.0000367. СКО приращений ASK = 0.0000409
и т.д.
Собственно, ни для кого не секрет, что истинным временем рынка является именно количество событий на единицу астрономического времени.
Поэтому, подставляя в формулу Sigma*sqrt(T) в качестве Т — количество реальных событий (цен CLOSE в сформированных барах), получаем следующие значения стандартного отклонения самого рыночного процесса:
1) Для S1. СКО цены BID = 0.00512. СКО цены ASK = 0.00570
2) Для S2. СКО цены BID = 0.00511. СКО цены ASK = 0.00571
3) Для S3. СКО цены BID = 0.00513. СКО цены ASK = 0.00572
и т.д.
Как видим, как бы мы ни прореживали ВР, какие бы бары ни рассматривали, СКО именно самого рыночного процесса остается практически неизменным и удовлетворяет основному закону случайных процессов — «корню из времени».
Хорошо это или плохо? Где деньги, дядя???!!!!!
А я чё, знаю?! У Колдуна спросите.
До встречи.
Toddler.
И все ж таки — какой же на рынке процесс? Случайный али нет? Есть ли хотя бы надежда припасть к Граалю и напиться из него Счастия?
Собственно говоря, неважно — какое именно уравнение описывает динамику рынка:
марковское
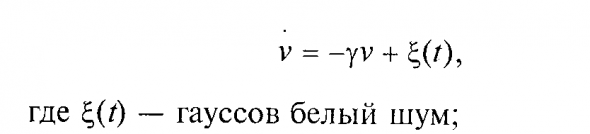
или немарковское:
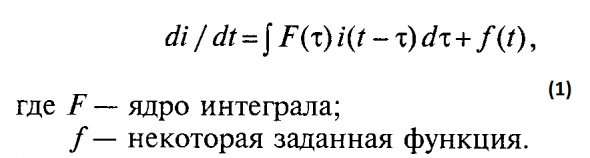
все равно — в правой части этих уравнений к некой прямой линии (сносу, дрифту,...) или скользящей средней всегда прибавляется случайная компонента, интеграл которой образует т.н. «случайное блуждание» и бороться с которым чрезвычайно трудно.
Именно поэтому, абсолютное большинство трейдеров пытаются наполнить карманы наличными, работая «по тренду», т.е. учитывать дрифт цены, либо взирая на поведение SMA, к примеру. А на случайную компоненту стараются не обращать внимания. Хе-хе… Как будто это так просто...
«Постойте!» — возопит особо внимательный страждущий.
«Как же это вы говорите, что для немарковского представления рынка, f(t) — случайная функция, а черным по белому написано, что f(t) — некоторая заданная функция!»
К сожалению — нет. На рынке f(t) — это именно случайная функция, дисперсия которой удовлетворяет зависимости Sigma*sqrt(T), свойственной именно полностью случайным процессам.
Рассмотрим, например, распределение приращений пары AUDUSD за 21 сентября 2020 г. Я даже приводить его гистограмму не буду — оно и так всем известно: островершинное и толстохвостое. Работать будем с архивом котировок от Dukascopy.
1) При анализе цен CLOSE 1-секундных (1S) баров имеем за сутки 34649 таких значений. СКО приращений BID = 0.0000275. СКО приращений ASK = 0.0000306
2) При анализе цен CLOSE 2-секундных (2S) баров имеем за сутки 24694 таких значений. СКО приращений BID = 0.0000325. СКО приращений ASK = 0.0000363
3) При анализе цен CLOSE 3-секундных (3S) баров имеем за сутки 19488 таких значений. СКО приращений BID = 0.0000367. СКО приращений ASK = 0.0000409
и т.д.
Собственно, ни для кого не секрет, что истинным временем рынка является именно количество событий на единицу астрономического времени.
Поэтому, подставляя в формулу Sigma*sqrt(T) в качестве Т — количество реальных событий (цен CLOSE в сформированных барах), получаем следующие значения стандартного отклонения самого рыночного процесса:
1) Для S1. СКО цены BID = 0.00512. СКО цены ASK = 0.00570
2) Для S2. СКО цены BID = 0.00511. СКО цены ASK = 0.00571
3) Для S3. СКО цены BID = 0.00513. СКО цены ASK = 0.00572
и т.д.
Как видим, как бы мы ни прореживали ВР, какие бы бары ни рассматривали, СКО именно самого рыночного процесса остается практически неизменным и удовлетворяет основному закону случайных процессов — «корню из времени».
Хорошо это или плохо? Где деньги, дядя???!!!!!
А я чё, знаю?! У Колдуна спросите.
До встречи.
Toddler.
Читайте на SMART-LAB:

GBP/USD: «Старый джентльмен» поймал попутный ветер
«Кабель» оттолкнулся от пробитого нисходящего канала, сформировав при этом свечную модель «Бычье поглощение» (хотя, учитывая вторую свечу в виде креста, точнее будет назвать её «Утренней звездой...
15.02.2026

Всё выше. Или как изменились средние доходности облигаций (по рейтингам) за неделю
Всё выше и выше, и выше. Средние доходности облигаций в зависимости от рейтинга (бледные столбцы — доходности без сглаживания). И как они изменились за неделю.
Телеграм:...
15.02.2026

Mozgovik Weekly. Комментарий по ключевым новостям недели.
Здравствуйте! Комментарий по ключевым событиям недели.
Сбербанк показал сильные результаты за январь 2026 года: рост прибыли обеспечен основными доходами при сохраняющемся высоком ROE...
15.02.2026

Интер РАО. Неужели дивиденды будут минимальными за 3 года? Обзор производственных результатов и отчета РСБУ за Q4 2025г.
Вышел отчет по РСБУ за Q4 2025г. от компании Интер РАО: 👉Выручка — 15,49 млрд руб.(-14,0% г/г)
👉Себестоимость — 12,79 млрд руб.(-10,8% г/г)
👉Валовая прибыль — 2,70 млрд руб.(-26,7% г/г)...
15.02.2026










Однако, скажите Холмс, почему случайный член имеет нормальное распределение? Это Vizard нашептал? Или Wizard?
С уважением
P.S. Ну и (чтобы 2 раза не вставать), почему стохастический компонент оказывает линейное влияние на цену?
потом, правда, после правильно сформулированного ответа… 4 Капитана могут на копьях понести…сами знаете куда…
ЗЫ Напиться из Грааля. М-да. А вы знаете что в нем налито? Когда узнаете, припадать, а уж тем более пить вряд ли захочется. Хотя… вкусы у всех разные.)