Блэк-Шоулз на уровне 10 класса средней школы

Не знаю, как сейчас, а в мое время простейшие свойства интегралов и производных проходили в 10 классе средней школы. Не верите? Ну найдите учебник по алгебре для 10 класса второй половины 70-х.

Нет, конечно интегралов будет недостаточно. Надо немножко знать теорию вероятностей, а именно что представляет из себя среднее (математическое ожидание) произвольной функции по некоторому распределению аргумента. Ещё из теории вероятностей нам потребуется определение нормального распределения, которое конечно в школе тоже не проходят. 

Итак, пара общих определений.
Платежное поручение — это обязательство продавца выплатить некоторую сумму покупателю, зависящую от  цены базового актива в будущий момент времени Т — С(Т).
Платежной функцией платежного поручения называется функция выплат f(C(T)).

Тогда справедливой ценой платежного поручения можно считать среднее f(C(T)) по распределению будущей цены С(Т) (чаще всего неизвестному точно), деленную на 1+R, где R- безрисковая ставка до момента времени Т.

Что такое справедливая цена в приведенном определении? Она означает, что если сделка будет проведена по этой цене, то средний выигрыш покупателя будет равен безрисковой ставке, а средний проигрыш продавца — той же безрисковой ставке. Почему возникает безрисковая ставка при «справедливости»? Это очень просто: покупатель платежного поручения вместо покупки может разместить средства под безрисковую ставку, а продавец платежного поручения, получив средства от продажи, также может разместить эти средства под безрисковую ставку и, соответственно, в среднем ничего не проиграть.

А как из сказанного возникает известная формула Блэка-Шоулза? А очень просто. Функция выплат по опциону колл со страйком S такая


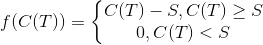
Каким может быть будущее распределение цен? Предположим, что приращение натурального логарифма цены имеет нормальное распределение со средним а и дисперсией сигма в квадрате


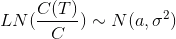
Тогда, чтобы взять среднее, нам надо представить функцию выплат, как функцию от приращения логарифма цены. Это просто. Из свойств логарифма (9-й класс средней школы в мое время) мы легко получим



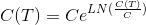
где С — текущая цена

И отсюда сразу получаем функцию выплат, как функцию от приращения логарифма цены и известных текущей цены С и страйка S




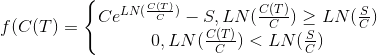
Для дальнейших выкладок нам понадобится одно обозначение уже из курса теории вероятностей для нормального распределения, а именно «размер» «хвоста распределения»



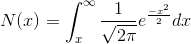
Обозначим LN(S)-LN( C ), как s маленькое.

Тогда справедливая цена, умноженная на 1+R, перепишется в виде интеграла



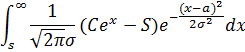
Произведем в нем замену х-а на х (10-й класс средней школы) 


 
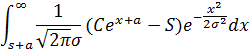
И еще одну замену  на х





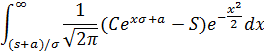
Теперь все готово, чтобы выразить справедливую цену, умноженную на 1+R, через функцию N(х)


 

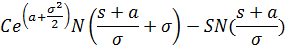
Ну вернем назад безрисковую ставку и получим формулу справедливой цены опциона колл, как функцию от а и сигма



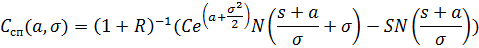
А как из нее получить формулу Блэка-Шоулза? Для этого надо сделать несколько дополнительных предположений об 1+R, а и сигма. А именно


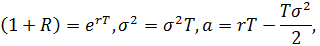
Отметим, что вторые две формулы имеют место в случае, когда приращения логарифмов LN(C(t+1))-LN(C(t)), t=0,...,T-1, С(0)=С, представляют из себя последовательность независимых нормально распределенных случайных величин со средним 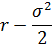 и дисперсией . 

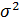Также отметим, что если приращения логарифмов цен просто независимые случайные величины с указанными постоянными средними и дисперсиями, то из центральной предельной теоремы для T>30 мы получим, что  распределение LN(C(T))-LN( C ) близко к нормальному с указанными средним и дисперсией. Так что и в этом случае формула Блэка-Шоулза, хоть и приближенно, но «работает».

А откуда берется равенство среднего LN(C(t+1))-LN(C(t)) величине 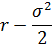 при дисперсии ?

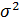А очень просто: если имеет место это равенство для среднего нормально распределенной величины LN(C(t+1))-LN(C(t)), то среднее относительного приращения (C(t+1)-С(t))/С(t) равно r, т. е. в среднем цены прирастают на безрисковую ставку.

Но мы получили несколько более широкую формулу справедливой цены для случая нормальности



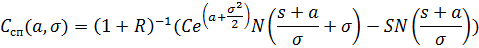
 из которой мы можем получать справедливые цены и при других моделях будущих а и сигма. Мы вообще можем предположить, что эти величины также являются случайными с плотностями g и h, соответственно. И тогда формула справедливой цены опять выразится через интеграл


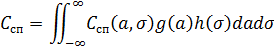
Но это уже другая история, как и вывод формул для более сложных платежных поручений.

Ну и где тут «безарбитражность» и прочая лабуда с частными производными?