С чего начинается математика
С чего начинается математика
Задачки из моего детства, для любого возраста, начиная с младшего школьного. Без контроля времени и отвечать не требуется. Многие их знают, некоторые совсем заезжены. Лучше не гуглить, тогда интернета не было, но передать другому – можно, особенно детям. Пусть не решат или не сразу, но подумают.
1. Для любителей спиртного
— Что ты любишь больше: водку или вино?
— Пиво!
Три трейдера SL освоили небольшой бизнес, производят водку, вино и пиво и хотят поставлять продукцию в три магазина, естественно, по трубопроводам.
3х3 = 9 трубопроводов надо провести без пересечений, не зарывая их и не поднимая, все только по поверхности.
Мне эта задачка в невинной детской формулировке досталась в третьем классе. Именно с нее началось мое увлечение математикой. Может, кто поделится своими воспоминаниями о первых математических задачках.
Для детей спиртное замените на что-нибудь более подходящее.
2. Для любителей геометрии
“Стоит четырехэтажный дом, в каждом этаже по восьми окон, на крыше — два слуховых окна и две трубы, в каждом этаже по два квартиранта. А теперь скажите, господа, в каком году умерла у швейцара его бабушка?” — Задачка бравого солдата Швейка (эпиграф)
Из точки А на юг вылетел самолет, пролетел 1000 км и оказался в точке B, там он повернул на восток, пролетел 1000 км и оказался в точке C.
Внизу летчик заметил медведя. Какого цвета был медведь, если AB=AC.
А эта попалась в четвертом классе. Похожа на задачку Швейка из эпиграфа?
3. Шахматная задача
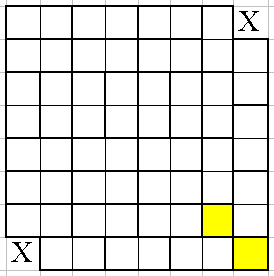
Из шахматной доски вырезают две угловые клетки одной диагонали. Замостить оставшуюся область двухклеточными костяшками домино, как бы так
Пример неудачной попытки, две помеченные желтым цветом клетки не накрылись одной костяшкой.
4. Для любителей теорвера
Кнопку какого этажа в лифте жители нажимают чаще всего.
Обнаружил, что дети не понимают теорвер.
5. Для любителей путешествий
Самолет. Кругосветный полет по кольцевому фиксированному маршруту с несколькими аэропортами. По пути движения он дозаправляется в этих аэропортах, забирая все имеющееся топливо. Суммарного топлива хватает на весь маршрут. Можно ли найти аэропорт, начиная с которого он сумеет успешно замкнуть кольцо. Топливо расходуется равномерно, ветра нет, никаких других самолетов, топливо не уходит налево, никаких аномалий, это математическая задачка, а не жизненная.
К этой задачке в жизни я возвращался несколько раз, не нравились найденные решения. И только немного освоив трейдинг я нашел то, которое меня устроило (трейдинг явно усилил меня). Трейдинг переключил меня с чисто математических на другие задачки, больше исследовательские и созидательные (ими то я как раз и занимался всю трудовую жизнь):
— как устроен рынок;
— как устроен “волшебный” индикатор за $300;
— что находится внутри зашифрованного робота;
— как ускорить работу алгоритма в 1000000 раз;
…
Их было очень много, было много нового, но и привычного тоже, и математике место нашлось.
Освоение дачи подкинуло набор практических задач, среди которых были две простые:
— установить два фундаментных блока на одном уровне, т.е. горизонтально, без использования специальных приборов, чисто подручными средствами. Обошелся треугольником. Расстояние между блоками – 3 м. Тоже детская задача.
— вычислить положение спутника НТВ+, рассчитать углы ориентации офсетной спутниковой тарелки и установить ее по этим углам без специальных приборов, только калькулятор. При кажущейся сложности это было просто, требовалась только точность, я сразу попал на спутник, без подгонки. Точность обеспечивал треугольниками больших размеров. Простая, но не для детей. Тут тригонометрия нужна. Проверил себя — теория не разошлась с практикой.
Был провал – не смог убедить местного электрика, что трехфазные 15 квт это хуже, чем однофазные. Даже ссылка на школьный принцип Дирихле с кроликами и попытка перейти к пределам (пытался объяснить на примере виртуального пятнадцатифазного электричества) не помогли.
Пара задачек помоложе, но тоже старые
6. На пространственное воображение
Есть ли странности в этой фигурке? Никаких склеек, естественно, нет. Вырезал из листа бумаги. Даже в качестве фокуса годится, можно рассматривать со всех сторон, только руками не трогать.
7. На топологические свойства материи
Тоже пришлось изготовить инвентарь. Карандаш с петлей из нерастягивающегося материала (шнурка, веревочки, провода), петля немногим меньше длины карандаша. Тоже годится как фокус. Здесь как раз можно трогать руками, потому, что я повешу инвентарь на петлицу, а его надо будет снять.
Видел радость одного парня, который сумел снять блокиратор со своего пиджака. Он вспоминал эту задачку даже много лет спустя.
















Представьте, что Вы учитесь не в четвертом, а в шестом классе и с Вас совсем другой спрос.
Я долго пытался отыскать эту брошюрку, но не преуспел.
Но как удачно, что я тогда на нее вышел.
Прямо «Значит, нужные книги ты в детстве читал».
Многие взрослые тоже не понимают. Или дают неверную интерпретацию. Или применяют формулу не понимая ее сути и области применимости.
Яркие примеры: парадокс двух конвертов и 3 двери (задача Монти-Холл).