Квадрат Экономии Данилиных QED
Квадрат Экономии Данилиных QED
Ошибки должны быть дешёвыми и для удешевления
проигрышей создан Квадрат Экономии Данилиных QED
заодно олицетворяющий актив и пассив ведь незачем
участвовать крупными суммами в возможных проигрышах.
Применяя Квадрат Экономии Данилиных QED происходит
ожидание выигрыша без крупных проигрышей и в итоге
получается дождаться событий с коэффициентом 100.
Квадрат Экономии Данилиных QED заполненный ставками
соблюдая правила ставок экономит затраты в десятки раз.
Квадрат Экономии Данилиных QED исключая азарт
олицетворяет догон многопоточный догон многоканальный.
Квадрат Экономии Данилиных
вариант ускоряющийся где за каждое
развитие выше вероятность выиграть
Ставки развиваются по горизонтали равными ставками
и по вертикали повышением ставок до уровня выше
и вновь переходят в ставки по горизонтали причём выигрыш
в любой точке поглощает в столбце все проигрыши ниже.
Квадрат Экономии Данилиных с постоянными вероятностями угадать
с постоянными множителями ставок при выигрыше после проигрыша
ведут к повышению выигрышей
Квадрат Экономии Данилиных с переменными вероятностями угадать
с переменными множителями ставок при выигрыше после проигрыша
ведут к понижению выигрышей
Несмотря на теорию единственной ставки в 1 время
возможны 2 ставки в 1 время при условии когда и выигрыш
и проигрыш ставки приводит к следующей ставке в нижней горизонтали
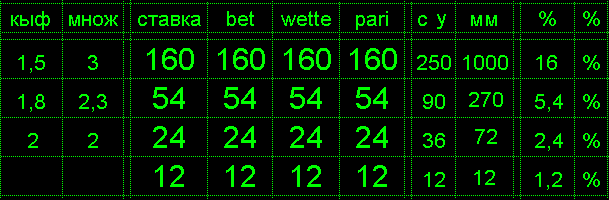
Применяется стратегия догон и догоняется коэффициент.
Отыграть сумму проигрышей возможно за несколько выигрышей
и выйдя в плюс лучше не отыгрывать бывшие проигрыши.
В общем виде математический финансовый менеджмент:
понижение коэффициента и повышение вероятности выигрыша
и повышая ставки по множителю зависимого от коэффициента.
При коэффициенте К множитель ставки М=1+(1/(К-1)).
При коэффициенте К=3 множитель ставки М=1+(1/(3-1))=1,5.
Для вероятности около 1/3 предел несовпадения подряд
равен Д=12 и при начальной ставке 1% на 12 ходу
ставка должна быть «1% умножить на М=1,5 в степени 12»
и получается ставка должна быть 130% баланса.
От коэффициента зависит множитель повышения следующей ставки.
От вероятности зависит число ставок до проигрыша баланса.
Математические законы справедливы во всех лотереях и
важно знать дюжину пределов несовпадения подряд наизусть.
Умножение постоянных вероятностей C+р^N=1
олицетворяет вероятность вероятности и создаёт формулу
N = LOG(1-C)/LOG(1-p)
С — вероятность выигрыша гарантированного
р — вероятность выигрыша события.
Например задача: число несовпадений подряд
с вероятностью 99% для вероятности 48,65%
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо возможно рассчитывать по формуле N = 7+(5*(1/x-2))
например х=0,1 N= 47 нормально и х=0,78 N= 4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Геометрические прогрессии содержащие в условии или в решении
смысл «в какую степень надо возвести» решаются через логарифм.
Используя предел несовпадения подряд в таблицах
обнаруживается волна или период угадываний 2-х видов:
1-й вид: волна или период — как сама вероятность
через количество тиражей и там где вероятность 1/3
там волна или период угадывания через 3 тиража;
2-й вид: волна или период — как предел несовпадений подряд
и там где вероятность 1/3 там волна или период угадывания
через 12 тиражей и возможно несколько ставок при сигнале.
Есть эмуляторы показывающие как динамично развивается
Квадрат Экономии Данилиных QED и при условии обнуления
значений ставок и при остановке при достижении выигрыша
Квадрат Экономии Данилиных QED показывает выигрышность
даже при применении одинаковых данных
для исследования каждой трети рулетки.
График ставок используя Квадрат Экономии Данилиных QED
выглядит как фрактал состоящий из волн составляющих
крупную волну и такой же график получается
при использовании математически обоснованных систем игры.
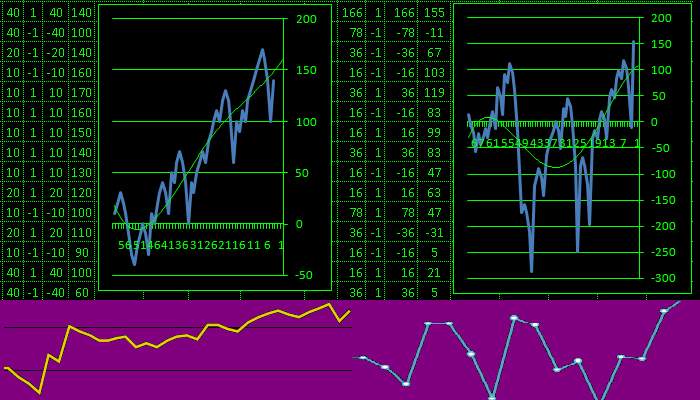
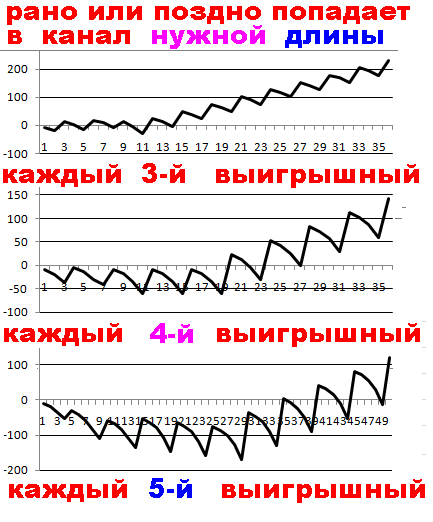
в моих темах развивается QEDbasic
и мозговой штурм ищет как распознавать иглы
и пока добавил счётчики удач и неудач
и рассчитываем деление несовпадений подряд
чтобы QEDbasic распознавалась игла меньше предыдущей
| вероятность | выиграть | 1 / … | 2 | 3 | 4 | 5 | 8 | 10 | 36 | 100 | 1,5 | 1,33 | 1 /… | win | probability | |||
| вероятность | проиграть | 50% | 67% | 75% | 80% | 88% | 90% | 97% | 99% | 33% | 25% | lose | probability | |||||
| несовпадений ПОДРЯД |
вероятность 1/… |
10 | 4 | 6 | 9 | 11 | 18 | 22 | 82 | 230 | 3 | 2 | 10 |
probability 1/... | discrepancies IN ROW |
|||
| несовпадений ПОДРЯД |
вероятность 1/… |
100 | 7 | 12 | 17 | 21 | 35 | 44 | 164 | 459 | 5 | 4 | 100 | probability 1/... | discrepancies IN ROW |
|||
| несовпадений ПОДРЯД |
вероятность 1/… |
1000 | 10 | 18 | 25 | 31 | 52 | 66 | 246 | 688 | 7 | 5 | 1000 | probability 1/... | discrepancies IN ROW |
|||
| несовпадений ПОДРЯД |
вероятность 1/… |
200 | 8 | 14 | 19 | 24 | 40 | 51 | 189 | 528 | 5 | 4 | 200 | probability 1/... | discrepancies IN ROW |
|||
| несовпадений ПОДРЯД |
вероятность 1/… |
50 | 6 | 10 | 14 | 18 | 30 | 38 | 139 | 390 | 4 | 3 | 50 | probability 1/... | discrepancies IN ROW |
|||
| несовпадений ПОДРЯД |
вероятность 1/… |
5 | 3 | 4 | 6 | 8 | 13 | 16 | 58 | 161 | 2 | 2 | 5 | probability 1/... | discrepancies IN ROW |
|||
| вероятность | выиграть | 1 / … | 2 | 3 | 4 | 5 | 8 | 10 | 36 | 100 | 1,5 | 1,33 | 1 /… | win | probability | |||
обновил QEDbasic строящий Квадрат Экономии Данилиных
создающий текстовые отчёты и возможно всё дополнять
внутри одного из отчётов анимация КЭД правильно надеюсь
особенность: считается вероятность и множитель
и далее возможны варианты ввода множителя или плюс/минус 10%
из массива считывается номер и определяется доля
от 1 по нужный номер и для других вариантов возможно менять
исходные данные со смещением или пересоздать массив номеров
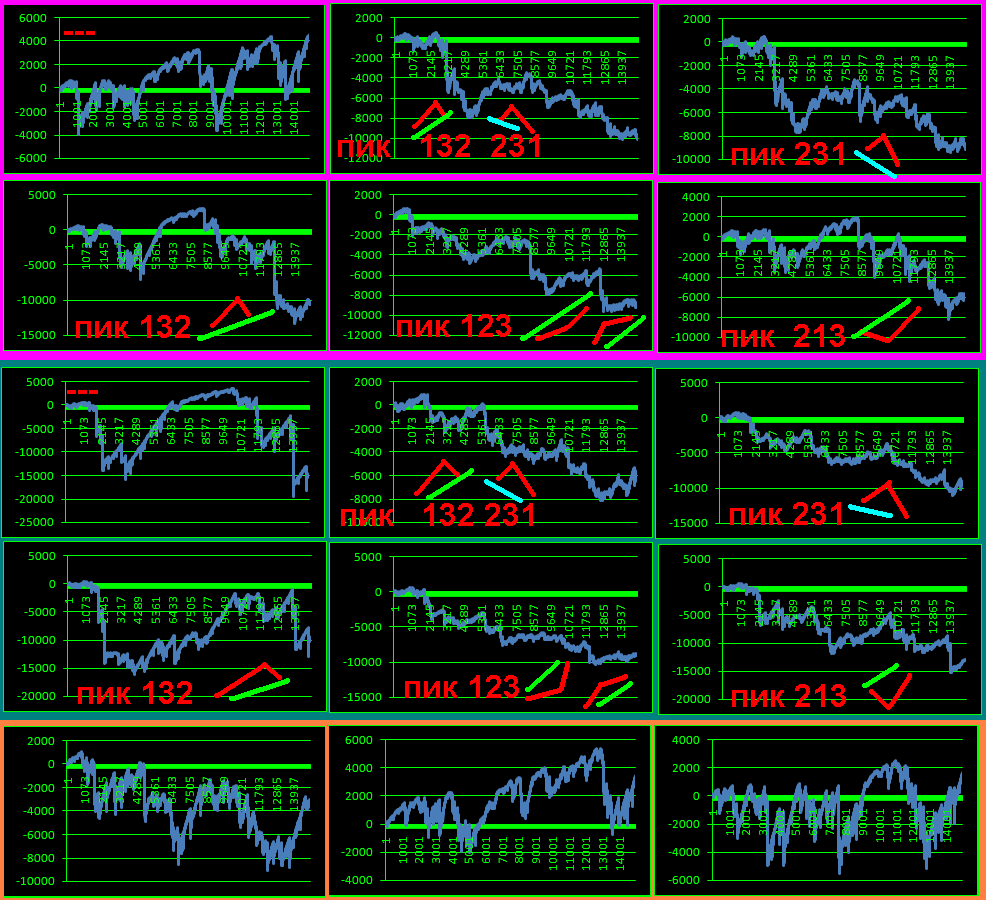
видим характерные виды графиков с углами и важнее волны
на графиках тестируемый массив на вероятностях 1: 2 3 4 1,5 1,33
и как видим проблема во временной неспособности эмулятора КЭД
распознавать иглу приводящую к обнулению КЭД лишь при максимуме
зато в прямом эфире человек может обнулять Квадрат Экономии Данилиных
обновил QEDbasic исследуя иглы
проще оказалось реализовать разделение по 100 тиражей
и в каждом отрезке смотреть 6 ситуаций из них 4 перспективных
и в принципе по схемам около букв на картинке ясно
мелкие отрезки оказались хуже и некоторые иглы и все иглы
тащили график вниз при любых номерах
дальше ещё исследую на разных вероятностях
и научусь применять деление несовпадений подряд
а пока перспективным оказался вид игла132:
баланс: наименьший / наибольший / средний
как понижение баланса когда локальная игла
обнуление только вертикали КЭД
при игла132: мало-много-средне
показывает перспективность исследований
в данном случае кыф 2 для 18/37 номеров
1. массив номеров заготовленный
2. массив номеров перевёрнутый
3. и 4. массивы номеров случайные
и далее исследую на других вероятностях
но каждый вариант вызывает дерево вариантов
игла132 подсказывает: старт и следим масимум и
чуть сложился игла132 буквально: половина между
началом и максимумом тогда обнулять столбец КЭД
означающий выиграла игла и дальше мало ставить
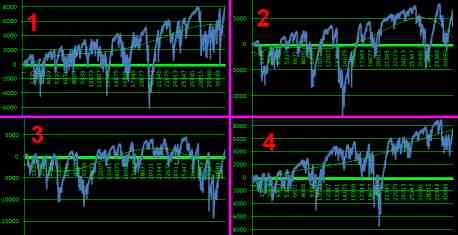
подтверждение моей теории
когда есть фаворит нечет чаще
из-за отсутствия доли чётных ничьих
особенно применив Квадрат Экономии Данилиных
Квадрат Экономии Данилиных содержит
точек проигрыша Х и точек выигрыша X^2-X
из чего возможно в будущем посчитать коэффициент
отдачи и возврат вложений для каждого
варианта КЭД в зависимости от стороны КЭД
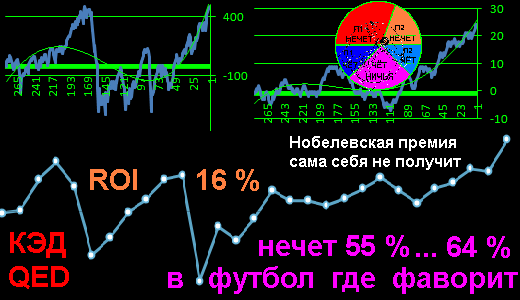
Нобелевская премия сама себя не получит















НЕ ПОНЯЛ НИЧЕГО!!!
и через час кто-то купил книжку на моём сайте
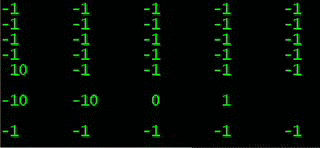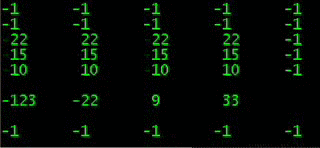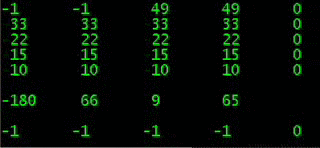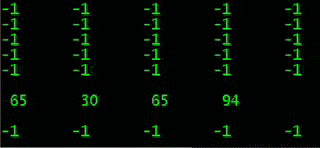
графическое изображение выгодности КЭД:
все возможные 64 варианта 6 случаев угадано / неугадано
догон: максимум: 6 & минимум: -63
Квадрат Экономии Данилиных: максимум 6 & минимум: -9
просто догон самый затратный
и разные уровни КЭД
гораздо экономичнее
треугольники между графиками и есть экономия
ведь в выражении Квадрат Экономии Данилиных
главное слово Экономии
и Квадрат главное и Данилиных тоже главное
все слова главные