Философия трейдинга. О некоторых «фокусах» из Ψизни «Епи».
«Одна из величайших трагедий нашего общества состоит в том, что в силу
страха перед премудростью, плохого преподавания или просто без всяких
причин поэзия математики и музыка природы скрыты от большинства людей.
Великолепные перспективы, которые открывает математика, недоступны
для них. Они могут восхищаться ароматом розы или буйством красок заката,
но ощутить всю полноту эстетического переживания им, увы, не дано.»
/Из книги известного английского учёного и популяризатора науки
Пола Дэвиса «Суперсила. Поиски единой теории природы.», 1989г./
Пожалуй, никто не станет отрицать того факта, что наша Природа-
матушка просто «влюблена» в «симметрии», о чём, собственно, и пишет
П. Дэвис в одной из глав своей книги. Потому с недавних пор с моей
стороны требуется симметричный ответ в отношении г-на
Бориса Гудылина. А, вот, собственно, и «ответка»! Как говорится,
«по мотивам и в развитие…» © :)))
Процитирую Б. Гудылина:
«Все изучают цены. Кому нужны эти непредсказуемые цены?
Не цены надо изучать, их и так изучают 99.99999% трейдеров, что очень
близко к печально известной цифре 95% (говорят, что депо сливают
на самом деле 99%)».
Потрясающая фраза! Большинство современных физиков – нет-нет!
речь идёт не о тех «физиках», о которых сейчас подумало большинство
трейдеров смартлаба, — с ней однозначно согласятся. Ведь, раньше было
как? Была «Золотая рыбка» и звали её – классическая математическая
физика. И все кликали Золотую рыбку. Приплывала Золотая рыбка и
спрашивала: «Чего тебе надобно, физик?» Ну, и понятно, надобно было
всегда одно – решить какое-нибудь «динамическое уравнение».
Например, такое (автономный осциллятор Ван дер Поля):
ẋ = у,
ẏ = -ω₀²х + μ(1- х²)у.
И всё было бы хорошо, но… Однажды появилась «Старуха»! И не просто
появилась, а возжелала быть Владычицей морскою, чтобы сама Золотая
рыбка была у неё на посылках! И, ведь, стала она Владычицей морскою!
Потому как не «динамические уравнения» (например, Шрёдингера или
Дирака) несут самую фундаментальную информацию о системе,
отнюдь не они! Кстати, звали ту Старуху – теория групп…
Теперь о проблеме… Её можно сформулировать в виде следующей цитаты,
взятой опять же у Б. Гудылина:
«Время жизни отдельного Фрактала – регулярности нет. Форма Фрактала –
регулярности нет, хотя есть и типовые варианты. Размеры фрактала –
регулярности нет.»
В пору, прям, поднять кверху лапки от такой оказии. Как сказал бы нам
домовёнок Кузя: «Ой, беда-беда! Огорчение!» Однако, дорогой мой
читатель, предлагаю не торопиться поспешно делать какие-либо выводы!
Ведь, сейчас вашему вниманию будет продемонстрирован самый настоящий
«фокус-покус», под названием «Регулярность – существует!»
Итак, будьте внимательны… поехали!
Перед Вами график, допустим RiH6. Таймфрейм – не имеет значения.
По оси Х – Время (t), по оси У – Цена (Р).
Накрываем график платочком. Читаем заклинание. (Что-нибудь из Гарри
Поттера вполне подойдёт.) «Deletrius Renatus Cartesius axis!»
Срываем платочек и что мы видим?
Время (t) и Цена (Р) «исчезли»! «Нет» ни оси Х, ни оси У! А чтобы Вам
было понятнее, что есть, пусть каждый представит себе для начала
электромагнитное поле так, как он его мыслит в силу своего уровня
образованности. Представили? Ну, так вот, перед нами вместо графика –
некий квантовый объект в некоем ценовом «калибровочном» поле.
Имеет ли квантовый объект структуру? Да, имеет.
Имеет ли место быть структурная устойчивость объекта? Однозначно,да.
Чем обусловлена данная структура объекта? Начальными условиями,
а именно – системами счисления и фундаментальными константами.
Регулярно ли поведение объекта? И да, и нет (суперпозиция).
Можно ли наблюдать исключительно регулярное поведение объекта?
Ответить на этот последний вопрос нам поможет оптика. Все помнят,
что такое линза? А гравитационная линза? Шучу! :)))
Представьте, что наша «регулярность» — это некий вектор О͞А.
(На самом деле это предельный цикл, но мы его «разрезали» и указали
направление, таким образом, получился вектор.) Поместим этот вектор перед
собирающей линзой на расстоянии равном двойному фокусному (2f),
как показано на рисунке:
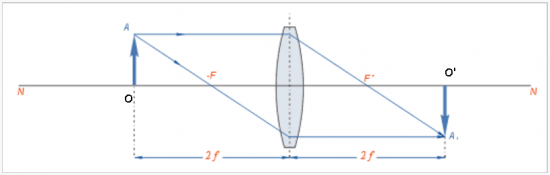
(рис. 1.)
Теперь рассмотрим варианты:
1) Дадим г-ну А. Шадрину в руки чистый лист бумаги («экран»). Каковы
будут его действия? Скорее всего он отмерит шагами ≥10-кратное фокусное
расстояние на котором и расположит свой «экран». Вопрос. Что он увидит?
Он увидит муть! Увидев последнюю, он бросит это дело, начнёт изучать
фундаментально-экономический анализ и станет инвестором.
2) А если алготрейдеру в руки дать «экран», где он его разместит?
Пожалуй, очень близко к линзе. Он, как и А.Шадрин, также увидит муть, но
муть совершенно иного рода – источник белого шума ξ(t) интенсивности D.
Ведь в реальных системах всегда присутствует шум в виде естественных
флуктуаций, обусловленных наличием «диссипации», а также в виде
случайных воздействий «внешней среды». Возможно также, что кроме шума
в нелинейной системе алготрейдер сыщет и некий источник гармонической
силы аCos(ω₁t + φ₀). Но в любом случае алготрейдер, особенно HFT, это
полезная «микрофлора», т.к., во-первых, «благотворно» влияет на
«здоровье» брокера и биржи, во-вторых, сами суть есть шум. Ибо в
литературе по нелинейной динамике имеются свидетельства того, что
внешний шум может повышать степень упорядоченности процессов
колебаний, выступая в роли конструктивного фактора. Как пример, явления
«стохастического резонанса» и «стохастической синхронизации».
3) Очень интересно посмотреть, к примеру, а где г-н В. Олейник
разместит свой «экран»? Вполне вероятно, что он может это сделать именно
на расстоянии равном 2f. Однако, «регулярность» он не разглядит, ибо
«фильтр», который он использует не подходит для этих целей. Однако,
именно тут и только тут «регулярность» и присутствует!
Кстати, уважаемый читатель, Вам вопрос на засыпку, вернее сказать,
маленькая гимнастика для серых клеточек мозга. Сколько элементов
содержит группа симметрии ансамбля объектов, представленного на рис.1?
А чтобы Вам не было обидно, скажу следующее: вопросов на засыпку,
которые я задаю сам себе – вагон и маленькая тележка. Один из
стратегических вопросов следующий. Можно ли применить вышеописанный
метод «структурного линзирования» для описания и прогнозирования
поведения объектов «небиржевого» характера? Из последних на ум
приходят – метеорологические и медико-биологические (в силу имеющегося
высшего медицинского образования).
В общем, как всегда! Вопросов больше, чем ответов.
П.С. Кстати, Вы спросите, а кто такой «Епи»? Знакомьтесь, это «Епи»:

П.П.С. Да, забыл упомянуть о «симметриях» следующее. Ли Смолин
в своей книге «Возвращение времени. От античной космогонии к
космологии будущего.» (2014г.) пишет о том, что «в природе не существует
фундаментальных симметрий». И что, мол, «хорошая» теория не должна
содержать никаких симметрий. Возможно он действительно прав и вот почему.
Если «грубо», то устойчивая структура биржевого квантового объекта имеет
симметрии. Но если подходить «тонко» к проблеме, то выясняется, что
симметрий то и нет! Нет! А «исчезнувшее» Время (t) и вправду возвращается
и лишь оно реально…














содержит группа симметрии ансамбля объектов
---
один. На плоскости симметрий может быть одна или две. Встречный вопрос вам, закон сохранения чего представлен у вас на рису.1? Любая симметрия соответствует закону сохрания.
Вся проблема применения всей туевой хучи способов торговли на фондовом рынке в том — что их нельзя применять в любое время.
Есть ведь простейший инструмент — статистика.
Даже наитопорнейшим методом собранный материалЪ о повторяющихся на рынке событий из раза в раз пропустить через вашу «призму» то эффект, результативность, профитабельность будет на порядок — лучше, выше, быстрее ...