28 апреля 2015, 16:22
Тест системы на неслучайность
Собственно, опишу критерий, по которому я сделал вывод о пригодности систем на основе EMA для торговли фьючерсами на индекс РТС и пару доллар-рубль. Сами рассуждения никоим образом не привязаны к этим конкретным инструментам, вся концепция не выходит за пределы статистики, то есть ее можно применять для оценки моделей любых случайных процессов и котировок чего угодно.
Для простоты рассмотрим цену на инструмент как случайный процесс с дискретным временем. Например, можно взять среднюю цену того же фьючерса за минуту и считать её ценой фьючерса в эту минуту. От минуты к минуте цена случайным образом изменяется, то в большую, то в меньшую сторону.
Время: 10:20:30, 10:20:31, 10:20:32, 10:20:33, 10:20:34, 10:20:35...
Цена: 1000, 1001, 1002, 1000, 998, 998, 997...
Приращение: 0, 1, 1, -2, -2, 0, -1...
В контексте торговли нам как раз интересна последовательность приращений цены. Можно взять не арифметическую разность соседних значений, а логарифм их отношений, суть от этого не меняется. Ведь в чём заключается процесс торговли: по сути мы берем график, выделяем на нём отрезки времени путём совершения сделок, далее эти выделенные куски вырезаем, те что в шорт переворачиваем и склеиваем их все вместе обратно. Цель процесса — чтобы полученный таким образом новый график рос быстрее, а падал медленнее, чем исходный.
Далее, опять же для простоты, предполагаем, что наша система совершает сделки только в лонг. Для каждого отдельного приращения, в соответствии с правилами системы, известно, открыта в данный момент времени сделка, или нет. Таким образом, торговая система по определенным правилам разбивает общее множество всех случайных ценовых приращений за определенный период на две выборки — те, что «внутри» сделки и участвуют в росте эквити системы, и те, что «снаружи», и не участвуют.
Так вот, мы, как разработчики торговой системы, принципиально хотим, чтобы средние значения у этих двух выборок различались. Иначе просто теряется смысл торговли по этой системе, с тем же успехом можно открывать и закрывать сделки случайным образом.
По счастью, для целей проверки гипотезы о различии средних значений двух выборок давным-давно придуманы статистические тесты. Нам интересен тест Стьюдента, вернее его модификация для двух выборок разного размера с необязанными совпадать дисперсиями, известная также как тест Уэлча. Ссылка на англоязычную Википедию: goo.gl/CTa5Jc.
Внимание, формула:
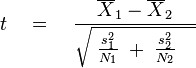
Здесь X1 и X2 с чёрточками — это средние значения, s1^2 и s2^2 — выборочные дисперсии, а N1 и N2 — количество элементов для первой и второй выборок, соответственно. Считаете эти параметры для каждой выборки, получаете конкретное значение t. Уже когда размеры обоих выборок составляют порядка нескольких десятков элементов, распределение значений t очень близко к нормальному с матожиданием 0 и дисперсией 1. Соответственно, чем больше абсолютное значение t для конкретной пары выборок, тем интереснее для нас та система, с помощью которой они были получены. Фактически, это количество «сигм», стандартных отклонений от матожидания нормального распределения для данной системы, показывающее вероятность того, что она ведёт себя на рынке случайным образом.
С увеличением периода тестирования и, соответственно, размеров выборок, у интересной системы критерий t постепенно растёт до интересных значений. Из практики и простого научного здравого смысла, начинаются эти значения где-то в районе шести (сигм). Системы с t меньше шести — скорее всего ни о чём. Те, о которых я писал в предыдущем посте, на EMAшках на минутках, дают порядка 8-9 сигм, и это только за период с середины марта для фьюча SiH5.
Вот так вот как-то так, умеющий читать да прочитает!
Всем профита (по мере сил).
Для простоты рассмотрим цену на инструмент как случайный процесс с дискретным временем. Например, можно взять среднюю цену того же фьючерса за минуту и считать её ценой фьючерса в эту минуту. От минуты к минуте цена случайным образом изменяется, то в большую, то в меньшую сторону.
Время: 10:20:30, 10:20:31, 10:20:32, 10:20:33, 10:20:34, 10:20:35...
Цена: 1000, 1001, 1002, 1000, 998, 998, 997...
Приращение: 0, 1, 1, -2, -2, 0, -1...
В контексте торговли нам как раз интересна последовательность приращений цены. Можно взять не арифметическую разность соседних значений, а логарифм их отношений, суть от этого не меняется. Ведь в чём заключается процесс торговли: по сути мы берем график, выделяем на нём отрезки времени путём совершения сделок, далее эти выделенные куски вырезаем, те что в шорт переворачиваем и склеиваем их все вместе обратно. Цель процесса — чтобы полученный таким образом новый график рос быстрее, а падал медленнее, чем исходный.
Далее, опять же для простоты, предполагаем, что наша система совершает сделки только в лонг. Для каждого отдельного приращения, в соответствии с правилами системы, известно, открыта в данный момент времени сделка, или нет. Таким образом, торговая система по определенным правилам разбивает общее множество всех случайных ценовых приращений за определенный период на две выборки — те, что «внутри» сделки и участвуют в росте эквити системы, и те, что «снаружи», и не участвуют.
Так вот, мы, как разработчики торговой системы, принципиально хотим, чтобы средние значения у этих двух выборок различались. Иначе просто теряется смысл торговли по этой системе, с тем же успехом можно открывать и закрывать сделки случайным образом.
По счастью, для целей проверки гипотезы о различии средних значений двух выборок давным-давно придуманы статистические тесты. Нам интересен тест Стьюдента, вернее его модификация для двух выборок разного размера с необязанными совпадать дисперсиями, известная также как тест Уэлча. Ссылка на англоязычную Википедию: goo.gl/CTa5Jc.
Внимание, формула:
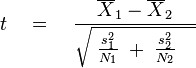
Здесь X1 и X2 с чёрточками — это средние значения, s1^2 и s2^2 — выборочные дисперсии, а N1 и N2 — количество элементов для первой и второй выборок, соответственно. Считаете эти параметры для каждой выборки, получаете конкретное значение t. Уже когда размеры обоих выборок составляют порядка нескольких десятков элементов, распределение значений t очень близко к нормальному с матожиданием 0 и дисперсией 1. Соответственно, чем больше абсолютное значение t для конкретной пары выборок, тем интереснее для нас та система, с помощью которой они были получены. Фактически, это количество «сигм», стандартных отклонений от матожидания нормального распределения для данной системы, показывающее вероятность того, что она ведёт себя на рынке случайным образом.
С увеличением периода тестирования и, соответственно, размеров выборок, у интересной системы критерий t постепенно растёт до интересных значений. Из практики и простого научного здравого смысла, начинаются эти значения где-то в районе шести (сигм). Системы с t меньше шести — скорее всего ни о чём. Те, о которых я писал в предыдущем посте, на EMAшках на минутках, дают порядка 8-9 сигм, и это только за период с середины марта для фьюча SiH5.
Вот так вот как-то так, умеющий читать да прочитает!
Всем профита (по мере сил).
56 Комментариев
 Тихая Гавань28 апреля 2015, 16:23а как вам не ЕМА а WMA?0
Тихая Гавань28 апреля 2015, 16:23а как вам не ЕМА а WMA?0 AlexFox28 апреля 2015, 16:43JMA точнее если уж так нравятся эти машки0
AlexFox28 апреля 2015, 16:43JMA точнее если уж так нравятся эти машки0 Аккаунт Удален28 апреля 2015, 16:56Дайте ему в профиль медальку «Профессор»+3
Аккаунт Удален28 апреля 2015, 16:56Дайте ему в профиль медальку «Профессор»+3 Costa28 апреля 2015, 17:32прочитал всё, но понял только концовку )0
Costa28 апреля 2015, 17:32прочитал всё, но понял только концовку )0
Читайте на SMART-LAB:

EUR/USD: коррекция перед очередным витком роста?
Европейская валюта отходит от недавно достигнутых максимумов. Цена корректируется и уже коснулась горизонтального уровня 1.1920. При пробое указанной отметки котировки могут «нырнуть» еще глубже,...
29.01.2026

Итоги первичных размещений ВДО и некоторых розничных выпусков на 29 января 2026 г.
Следите за нашими новостями в удобном формате: Telegram , Youtube , RuTube, Smart-lab , ВКонтакте , Сайт
29.01.2026










