06 июня 2013, 15:15
Толстые хвосты и эмпирические распределения
Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра.
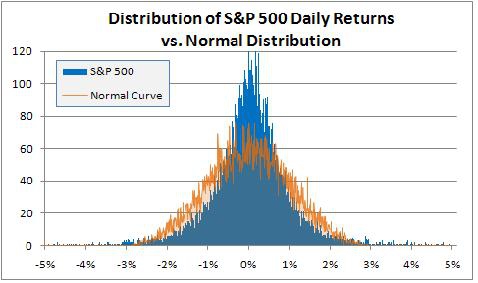
Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже
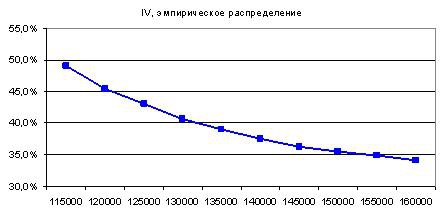
Откуда, по вашему мнению, на графике выше появилась улыбка? Из-за толстых хвостов! – наверняка скажут многие. Тогда, спрошу я, откуда же берется улыбка на рисунке ниже?
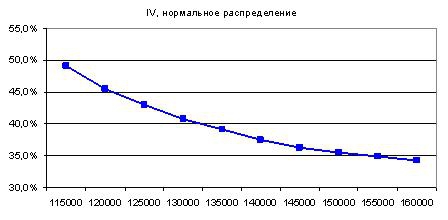
График построен не по эмпирическому распределению, а по нормальному, но с теми же параметрами, как и эмпирическое (матожидание и среднекв. отклонение). Параметры рассчитаны для нашего ряда логарифмов. Конечная цена фьючерса для эмпирического распределения определяется по формуле
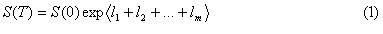
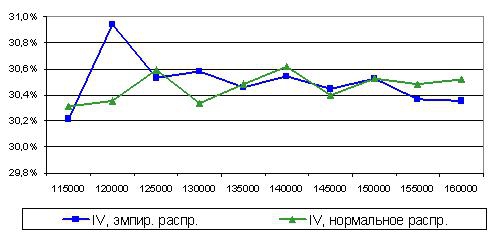
где li –логарифм Ln( S(i)/S (i-1)), случайно выбранный из нашего ряда.Для нормального распределения меняем li на ni
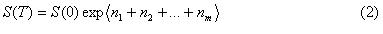
где ni – нормальная величина (0; ср.отклонение ряда li.)
Откуда же взялась улыбка там, где ее не должно быть?
Ответ в том, что, хотя нам казалось, что по построению мы исключили тренд, на самом деле положительный тренд возник. Ведь если цена непрерывно движется по броуновскому закону, как предполагается в модели БШ,

то c течением времени у логарифма цены возникает тренд

То есть, матожидание Ln(S(T)) – Ln(S(0)) равно (4). А у нас, напомню, эмпирическое распределение выбрано из ряда, в котором начальная и конечная цены совпадают, и, как следствие, матожидание Ln(S(T)) – Ln(S(0)) равно нулю . Таким образом, в нашем опыте с точки зрения модели БШ актив движется с положительным трендом µ, равным σ* σ /2 (T-t). Тренд повлиял на стоимость опционов колл, причем прирост стоимости опционов дальних страйков из-за тренда оказался не менее сильным (а по факту даже большим), чем для ближних. Искажение цен опционов привело к возникновению улыбки.
Замечу, что сам расчет цены опционов и их волатильности был некорректен. Если существует тренд, отличный от безрисковой ставки (которая для фьючерсов равна нулю), то инвестор не нейтрален к риску, ведь для риск-нейтрального инвестора все активы приносят один доход, равный безрисковой ставке. Если инвестор не риск-нейтрален, то считать стоимость опциона методом усреднения модельных терминальных цен нельзя, т.к. такой инвестор оценивает ценность прибыли и убытка по-разному. Внесем коррекцию, добавим тренд -σ* σ /2 (T-t) к эмпирическому и нормальному распределениям и нарисуем соответствующие улыбки
Мы видим, что отличия в улыбках минимальны. Они объясняются случайной ошибкой в рамках модели. Волатильность слева более чувствительна к ошибкам, поэтому размах колебаний выше. Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки на данном временном интервале. Замечу, что и в случае нескорректированной на тренд модели, отличия между двумя улыбками также минимальны и объясняются случайными ошибками.
Любопытно, что аналогичные выводы получаются, если использовать не эмпирическое, а другое распределение цен с толстыми хвостами, имеющее конечную дисперсию и матожидание. В частности, похожий опыт был когда-то поставлен мной для распределения Пирсона седьмого порядка с куртозисом, взятым из рыночного распределения. В этом случае улыбка также вырождается в прямую линию.
Причина отсутствия улыбки – Центральная Предельная Теорема, смысл которой состоит в том, что сумма независимых, одинаково распределенных случайных величин стремится в пределе к нормальному распределению. В нашем случае сумма величин li в формуле (1) дает величину, близкую к нормальной, в связи с большим периодом модели, равным ста шагам. Вопрос о меньшем количестве шагов модели будет рассмотрен в другой статье.
Эмпирическое распределение может быть построено и для приращений актива, которые не являются независимыми. В частности, в журнале ФиО n1-2 за 2009г. Израйлевичем и Цудикманом была представлена модель оценки опционов на основе доходности актива за периоды, равные времени до экспирации. Однако, применяя рассуждения, аналогичные изложенным выше, мы убедимся, что использование исторических рядов цен в общем случае приведет к возникновению тренда и искажению стоимости опционов в модели. Для более точной оценки модель должна быть скорректирована на тренд.
Выводы:
1. Эмпирическое распределение для оценки стоимости опционов следует применять с коррекцией на тренд.
2. В модели ежедневных независимых приращений цен актива, построенной на основе исторических данных, улыбки волатильности не возникает при сроках до экспирации выше 100 дней.
Ссылки
график ежедневных доходностей S&P 500 взят с сайта
http://managed-futures-blog.attaincapital.com/

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

Откуда, по вашему мнению, на графике выше появилась улыбка? Из-за толстых хвостов! – наверняка скажут многие. Тогда, спрошу я, откуда же берется улыбка на рисунке ниже?

График построен не по эмпирическому распределению, а по нормальному, но с теми же параметрами, как и эмпирическое (матожидание и среднекв. отклонение). Параметры рассчитаны для нашего ряда логарифмов. Конечная цена фьючерса для эмпирического распределения определяется по формуле
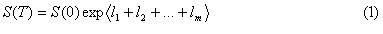
где li –логарифм Ln( S(i)/S (i-1)), случайно выбранный из нашего ряда.Для нормального распределения меняем li на ni
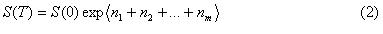
где ni – нормальная величина (0; ср.отклонение ряда li.)
Откуда же взялась улыбка там, где ее не должно быть?
Ответ в том, что, хотя нам казалось, что по построению мы исключили тренд, на самом деле положительный тренд возник. Ведь если цена непрерывно движется по броуновскому закону, как предполагается в модели БШ,

то c течением времени у логарифма цены возникает тренд

То есть, матожидание Ln(S(T)) – Ln(S(0)) равно (4). А у нас, напомню, эмпирическое распределение выбрано из ряда, в котором начальная и конечная цены совпадают, и, как следствие, матожидание Ln(S(T)) – Ln(S(0)) равно нулю . Таким образом, в нашем опыте с точки зрения модели БШ актив движется с положительным трендом µ, равным σ* σ /2 (T-t). Тренд повлиял на стоимость опционов колл, причем прирост стоимости опционов дальних страйков из-за тренда оказался не менее сильным (а по факту даже большим), чем для ближних. Искажение цен опционов привело к возникновению улыбки.
Замечу, что сам расчет цены опционов и их волатильности был некорректен. Если существует тренд, отличный от безрисковой ставки (которая для фьючерсов равна нулю), то инвестор не нейтрален к риску, ведь для риск-нейтрального инвестора все активы приносят один доход, равный безрисковой ставке. Если инвестор не риск-нейтрален, то считать стоимость опциона методом усреднения модельных терминальных цен нельзя, т.к. такой инвестор оценивает ценность прибыли и убытка по-разному. Внесем коррекцию, добавим тренд -σ* σ /2 (T-t) к эмпирическому и нормальному распределениям и нарисуем соответствующие улыбки

Мы видим, что отличия в улыбках минимальны. Они объясняются случайной ошибкой в рамках модели. Волатильность слева более чувствительна к ошибкам, поэтому размах колебаний выше. Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки на данном временном интервале. Замечу, что и в случае нескорректированной на тренд модели, отличия между двумя улыбками также минимальны и объясняются случайными ошибками.
Любопытно, что аналогичные выводы получаются, если использовать не эмпирическое, а другое распределение цен с толстыми хвостами, имеющее конечную дисперсию и матожидание. В частности, похожий опыт был когда-то поставлен мной для распределения Пирсона седьмого порядка с куртозисом, взятым из рыночного распределения. В этом случае улыбка также вырождается в прямую линию.
Причина отсутствия улыбки – Центральная Предельная Теорема, смысл которой состоит в том, что сумма независимых, одинаково распределенных случайных величин стремится в пределе к нормальному распределению. В нашем случае сумма величин li в формуле (1) дает величину, близкую к нормальной, в связи с большим периодом модели, равным ста шагам. Вопрос о меньшем количестве шагов модели будет рассмотрен в другой статье.
Эмпирическое распределение может быть построено и для приращений актива, которые не являются независимыми. В частности, в журнале ФиО n1-2 за 2009г. Израйлевичем и Цудикманом была представлена модель оценки опционов на основе доходности актива за периоды, равные времени до экспирации. Однако, применяя рассуждения, аналогичные изложенным выше, мы убедимся, что использование исторических рядов цен в общем случае приведет к возникновению тренда и искажению стоимости опционов в модели. Для более точной оценки модель должна быть скорректирована на тренд.
Выводы:
1. Эмпирическое распределение для оценки стоимости опционов следует применять с коррекцией на тренд.
2. В модели ежедневных независимых приращений цен актива, построенной на основе исторических данных, улыбки волатильности не возникает при сроках до экспирации выше 100 дней.
Ссылки
график ежедневных доходностей S&P 500 взят с сайта
http://managed-futures-blog.attaincapital.com/
Читайте на SMART-LAB:
Клиенты рекомендуют Займер 💚
Клиентская лояльность — одна из ключевых метрик для компаний в сфере услуг. В случае банков и МФО высокая лояльность позволяет экономить на привлечении новых заемщиков — а это значительная статья...
04.03.2026

📄 Ресейл Инвест получил право проводить закрытые размещения акций
Банк России согласовал правила инвестиционной платформы Ресейл Инвест. Платформа сможет осуществлять деятельность в соответствии с требованиями законодательства Российской Федерации и...
04.03.2026












Я глубоко этим вопросом не занимался, но возможно стоит покопать в направлении оценок опционов под стохастической волатильностью или CEV-модели и т.д. Сейчас уже очень много понаридумывали альтернативных GBM процессов
Было бы интересно глянуть на аналогичные приведенным графики для 22 и 11 дней (месяц и полмесяца). 100 дней (4.5 месяца) — большой и довольно странный выбор срока. В первую очередь интересуют уже очищенные от тренда, так как иначе некорректно говорить об одной улыбке в принципе. Причем есть предложение рисовать улыбку в обе стороны от денег, поскольку форма в разные стороны разная.
Кстати, если вы нарисуете для 100 дней вправо тоже (но том же графике, что влево), то небольшой наклон, который угадывается глазами и сейчас (если выкинуть 2 крайних точки), может стать более заметным. Это к фразе: «Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки». Мне из того же графика видится, что повлияли, только несильно (а чего еще ждать от 4 с лишним месяцев?...)