Returns vs Volatility (Attention! The article has the formula!)

Финансовые временные ряды помимо толстых хвостов в распределении доходностей часто демонстрирует так называемый эффект левериджа: когда волатильность возрастает со снижением рынка и, наоборот, снижается, когда рынок растет.
Влияет ли данный эффект на стоимость опционов? Попробуем разобраться.
Для этого, для начала, посчитаем коэффициент корреляции Пирсона для рядов однодневных доходностей и волатильности «на центральном страйке». Будем использовать рыночные данные для фьючерса на индекс РТС и его опционов (3/2010 — 5/2013). Причем будем рассматривать только опционы, до экспирации которых осталось от 45 до 5 календарных дней. Доходности будем получать по формуле: ret[t] = log(S[t]/S[t-1]). Волатильность «на центральном страйке» будем определять как IV0[t] = f(par[t], x=0),  где par[t] — вектор параметров функции f, описывающей рыночную улыбку на конец торгового дня t; x = log(K/S) — «денежность» опциона со страйком K при цене базового актива S.
Т.о. перед нами два ряда ежедневных логарифмических доходностей: ret[t] = log(S[t]/S[t-1]) и rvol[t] = log(IV0[t]/IV0[t-1]).
Коэффициент корреляции Пирсона для заданных временных рядов:
rho = -0.48 (коэффициент корреляции)
t = -17.8481, df = 1061, p-value < 2.2e-16 (t-статистика, число степеней свободы, вероятность — уровень значимости)
alternative hypothesis: true correlation is not equal to 0 (Гипотеза о нулевой корреляции отвергается)
95 percent confidence interval: -0.5254774 -0.4329139 (95% доверительный интервал для коэффициента корреляции)
Вывод: корреляция присутствует и равна -0.48 (по Пирсану)
Изобразим на графике анализируемые данные: ось X — ret[t], ось Y - rvol[t].
Также построим линейную регрессию: ret[t] = alpha + beta * rvol[t]

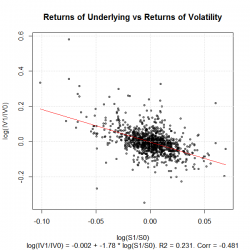
Мы получили следующие параметры регрессии:
/>
 
Estimate
Std. Error
t value
Pr(>|t|)

alpha
-0.00151
0.00191
-0.79
0.43

beta
-1.78004
0.099733
-17.85
<2e-16



Коэффициент beta получился значимым, alpha — не значимым. Коэффициент детерминации R2 = 0.23.
Мы показали, что опционы на фьючерс на индекс РТС подвержены влиянию так называемого эффекта левериджа: при падении базового актива на 1% стоит ожидать роста волатильности на 1.78% (подразумеваемой волатильности «центрального страйка»), и, наоборот, при росте фьючерса волатильность опционов как правило снижается.
Обращаю внимание, что в расчетах участвовали опционы, до экспирации которых оставалось от 45 до 5 календарных дней. Стоит учесть, что с уменьшением T — времени до экспирации увеличивается разброс значений вокруг линии регресии, что в свою очередь снижает точность оценки (прогноза) изменения волатильности. Это хорошо видно на представленных ниже рисунках.




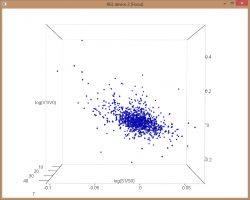
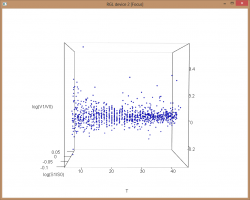
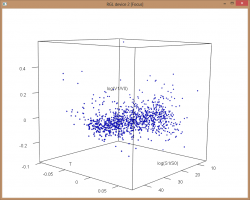
Расчеты были произведены для «центрального страйка», а как реагирует волатильность ITM и OTM опционов — читайте в следующей статье.

Оригинал статьи на quant-lab.com:
http://quant-lab.com/research/returns-vs-volatility.html