SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Информация
Торговые сигналы!
Торговые сигналы! | Фрактальный бар-о-метръ 24.12.2012
- 24 января 2013, 10:07
- |
Сегодня просто барометр.
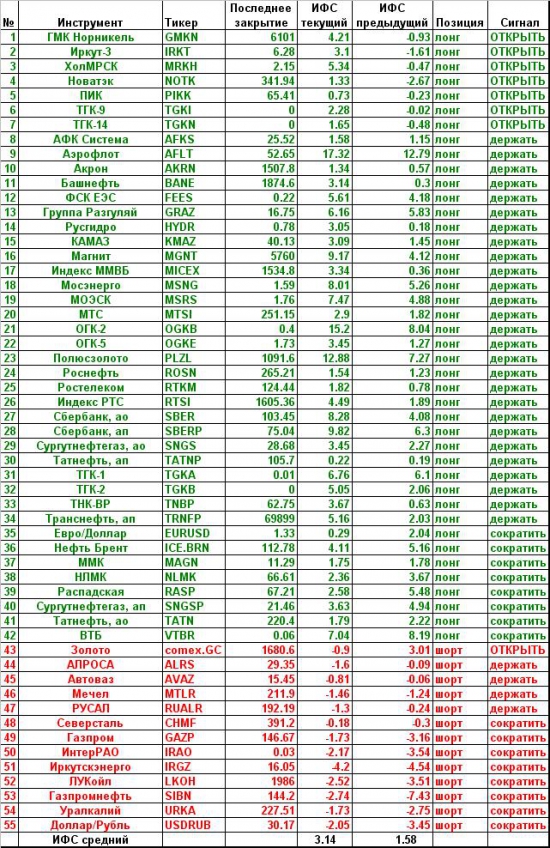
Сигналы таблицы основаны на значении фрактального индекса силы рынка. Описание индикатора здесь: www.dartstrade.ru/blog/gurilka/384.html
Положительное значение индекса означает преобладание на текущий момент покупателей в данной бумаге, отрицательное – преобладание продавцов. Изменение знака индикатора означает переход преимущества от покупателей к продавцам или наоборот и является сигналом для изменения позиции. Если Знак меняется с отрицательного на положительный то появляется сигнал на покупку (в таблице появляется строка ОТКРЫТЬ лонг), наоборот – сигнал на открытие короткой позиции (в таблице появляется строка ОТКРЫТЬ шорт). Если бумагу нельзя открыть в короткую позицию, то появление сигнала «ОТКРЫТЬ шорт» означает закрытие позиции и выход в деньги. Другие способы применения фрактального барометра здесь:www.dartstrade.ru/blog/gurilka/395.html
Сигналы таблицы основаны на значении фрактального индекса силы рынка. Описание индикатора здесь: www.dartstrade.ru/blog/gurilka/384.html
Положительное значение индекса означает преобладание на текущий момент покупателей в данной бумаге, отрицательное – преобладание продавцов. Изменение знака индикатора означает переход преимущества от покупателей к продавцам или наоборот и является сигналом для изменения позиции. Если Знак меняется с отрицательного на положительный то появляется сигнал на покупку (в таблице появляется строка ОТКРЫТЬ лонг), наоборот – сигнал на открытие короткой позиции (в таблице появляется строка ОТКРЫТЬ шорт). Если бумагу нельзя открыть в короткую позицию, то появление сигнала «ОТКРЫТЬ шорт» означает закрытие позиции и выход в деньги. Другие способы применения фрактального барометра здесь:www.dartstrade.ru/blog/gurilka/395.html
теги блога Mikola
- 2007
- 2011
- 2012
- 2013
- ROE
- алмаз
- анализ
- аналитики
- арсагера
- аукционы
- бар-о-метръ
- барометр
- бизнес
- ВВП
- волатильность
- воскресенье
- встреча
- выкуп акций
- Газпром
- госкомпании
- госсектор
- грааль
- давление
- дартстрейдинг
- девальвация
- девушки
- декабрь
- диапазон
- динамика
- Доу-Джонс
- елка
- импортозамещение
- индекс
- индикатор
- капитал
- капитализация
- книги
- кодекс
- колебания
- коллективный
- кондратьев
- конец
- корпоративное управление
- крым
- лажа
- либералы
- Луна
- Маркс
- медведев
- ММВБ
- налоги
- Не прогноз
- новолуние
- ноябрь
- октябрь
- опрос
- оффтоп
- поведение
- полнолуние
- прибыль
- приватизация
- прогноз
- производительность
- рабочее место трейдера
- рентабельность
- роботы
- Росимущество
- Россия
- рынка
- рынок
- сила
- случайность
- совет
- совет директоров
- сопротивления
- Социализм
- спекулянты
- США
- теханализ
- толпы
- топ-менеджмент
- торговля
- торговые сигналы
- трейдеров
- труд
- февраль
- фигуры
- фонд
- фондовый рынок
- фото
- фотографии
- фрактал
- фрактальность
- фрактальный
- циклы
- человек
- чиновники
- шадрин
- эндаумент
- юмор
Вопрос по формуле расчета вашего индикатора. В описании я этого не нашел.
Фрактальная размерность, которая лежит в основе вашего индикатора, рассчитывается на основе выборки за промежуток времени (N сэмплов). Ваш индикатор строиться по дням, а для определения фрактальной размерности, какой масштаб вы используете? Часы, минутки за пред. день? или дни?
я пробовал считать фрактальную размерность и когда читал на эту тему, вот например здесь capital-times.com.ua/index.php?option=com_content&task=view&id=11623&Itemid=88888963 сказано, что «При незначительных количествах наблюдений N фактические расчеты нормированного размаха R/S случайных рядов дают заметно заниженные результаты по сравнению с теоретическим R/S. Данное несоответствие порождает меньшие значения показателя Херста при малых N.»
Мне эта тема очень интересна, но я, что бы увеличить количество выборок, использовал минуты и более мелкие интервалы.
Да и чисто с позиции здравого смысла — какая размерность при анализе двух или четырех значений? Выборка слишком мала.
По второму вопросу. Если мы ничего не знаем о внутренней структуре, лежащей внутри этих двух, или четырех значений, то конечно нет никакого смысла. Но если мы знаем, что внутри двух дневных свечек у нас «спрятано» несколько десятков тысяч сделок, то вопрос приобретает смысл — расчет размерности по двум значениям агрегированных свечей является много чем. В частности:
1. Простейшей оценкой размерности на всем интервале (вероятнее всего завышенной)
2. Оценкой асимптотики поведения размерности на больших масштабах наблюдения (значение этой асимптотики сама по себе является значимой информацией)
3. Эвристическим индикатором принятия решений.
«Существует как минимум две вариации фрактальной размерности – D и A. Так, фрактальную размерность D [размерность временного следа – это оценка степени изломанности ряда] определяют по следующей формуле:
D = 2 – H. Бенуа Мандельброт (Benoît B. Mandelbrot) в своей работе2 показал, что фрактальная размерность является обратной величиной от H. Например, при H = 0.5 фрактальная размерность равна 2 (1/0.5), а при H = 0.8 фрактальная размерность равна 1.25 (1/0.8). Таким образом, фрактальную размерность по Мандельброту А [размерность пространства вероятностей – оценка толщины хвостов в функции плотности вероятности] рассчитывают по формуле: A = 1/H.»