Улыбка недельных опционов

Какая должна быть правильная форма улыбки? Продолжаю разбираться с этим вопросом, используя эмпирическое распределение. Как было показано в моих июньских постах, построенное по дням эмпирическое распределение не дает улыбку привычной рыночной формы. Вероятно, это связано с тем, что распределение не учитывает кластеризацию волатильности и коррелированность последовательных ежедневных приращений.
 
Чтобы исключить искажение из-за коррелированности приращений, рассмотрим распределение на основе недельных приращений цены. Распределение строится на основе пятидневных скачков индекса РТС, созданных с помощью скользящего окна с января 2010г. по февраль 2013г. Время до экспирации принимается равным одной неделе. В связи с возможным введением недельных опционов выбор недели в качестве временного интервала наиболее интересен.

В качестве базового актива выбран индекс, а не фьючерс, поскольку дельтахеджирование не производится, а излишняя волатильность фьючерса несколько искажает результат. Ставка доходности принимается равной нулю. Полагаю, это справедливо для долларового индекса. Для удобства работы каждое значение индекса увеличим на 100.

 
Коррекцию на тренд делаю другим способом, чем в предыдущих постах. Напомню, что ранее коррекция производилась с расчетом волатильности приращений. Должен признаться, что предложенный способ хорош только для логнормального распределения. Свойства «логэмпирического» распределения другие. Здесь перестает действовать формула вывода матожидания через параметры распределения под знаком логарифма. Впрочем, для ежедневных приращений ошибка минимальна, и выводы предыдущих статей сохраняют силу. Но ошибка для недельных приращений выше уже на целый порядок, что, вероятно, связано с серьезным отходом от нормального распределения.
 
Теперь я беру распределение не из ряда логарифмов Ln (S(i)/S(i-1)), а из ряда отношений цены S(i)/S(i-1). Вычитая из этого ряда среднее, получаю необходимые характеристики распределения
 
E(S(i)/S(i-1)) =1                                                                          (1)
 
E(S(T)) =  E(S(0))                                                                        (2)
 
Подобным же образом можно делать коррекцию тренда для повторяющихся интервалов, например для пяти недель. Свойство (2) сохранится, ведь матожидание произведения независимых величин равно произведению их матожиданий.
 
Начальной ценой для каждого эксперимента принимаем 150000 пунктов. Умножая это число на каждый член ряда приращений, получаем финальное значение цены. Страйки опционов, как обычно, расположены в точках 145000, 140000, 135000 и т.д.
 
1 способ расчета улыбки
Как обычно, строим множество цен базового актива на момент экспирации. Им соответствуют цены опционов на момент экспирации. Усредняем цены опционов. Учитываем, что ставка доходности равна нулю. Получаем стоимость опционов в начальный момент времени. Отсюда выводим график волатильности опционов с центральным страйком 150000. 

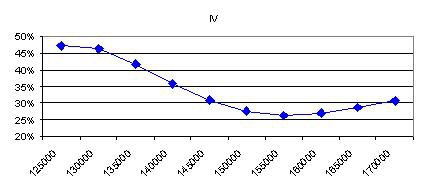
2 способ расчета улыбки
Полученный результат похож на реально наблюдаемую улыбку. Но можно ли доверять такому результату и утверждать, что улыбка за неделю до экспирации должна иметь подобную форму? Очевидно – нет! Улыбка построена с данными, взятыми из разных кластеров волатильности. Попытаемся исключить этот эффект, деля каждый член ряда приращений на текущую двадцатидневную HV и умножая на среднюю HV за весь период. Полученный график демонстрирует более сильный наклон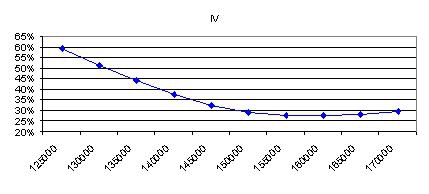
3 способ расчета улыбки
По сути, нас интересует не столько абсолютное значение волатильности, сколько наклон улыбки. Наклон можно найти, сравнивая волатильность каждого страйка с неким параметром в текущий момент времени. В качестве такого параметра возьмем двадцатидневную HV. Будем искать разницу между волатильностью выбранного страйка и выбранной HV. Задача – посчитать смайл для каждого страйка, где смайл определяется из формулы:

Волатильность страйка i = HV + смайл(i)

Решение задачи – смайл, дающий «наилучшую» начальную цену опциона. Этот смайл  минимизирует сумму ошибок: квадратов разности теоретических  (прогнозных в начальный момент времени) и практических цен опционов (стоимости опционов на экспирации) в каждой реализации эксперимента. Ниже — график полученных смайлов: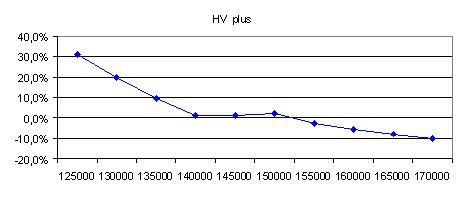
4 способ расчета улыбки
Аналогично строим график для смайлов, определяемых как разница волатильностей выбранного страйка и центрального страйка. В качестве волатильности центрального страйка возьмем IV центрального страйка квартальных опционов. Ниже — соответвующая формула и график смайлов.

Волатильность страйка i = IV(0) + смайл(i)


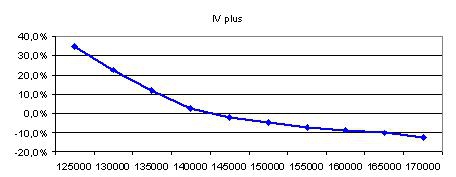
Какой способ лучше ?
Какой из четырех способов дает лучшее приближение улыбки? Определим это посредством минимизации суммарной ошибки. В качестве ошибки, как и раньше, я беру разность сумму ошибок: квадратов разности теоретических и практических цен опционов в каждой реализации эксперимента. В таблице ниже указаны ошибки для каждого способа по каждому страйку



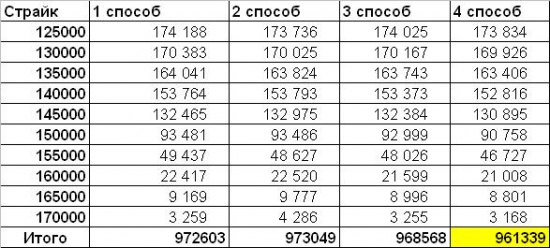
Очевидно, четвертый способ, рассчитывающий волатильность по отношению к центральному страйку, дает наилучшие результаты. Таким образом, наиболее точная форма улыбки представлена на четвертом графике. Ниже приведена табличка соответствующих смайлов в сравнении со смайлами реальных рыночных улыбок за неделю до экспирации. 



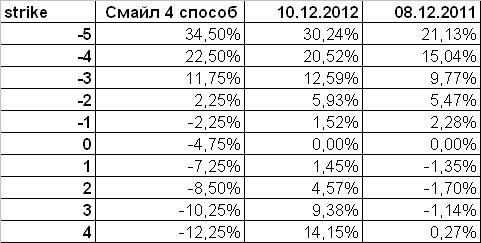
Таким образом, наиболее точной из рассмотренных является улыбка, основанная на эмпирическом распределении и вмененной волатильности квартальных опционов. Полученная улыбка имеет слева крутой наклон, заметно превышающий наклон реально наблюдаемых графиков. В отличие от рыночных улыбок, справа от центрального страйка подъема вверх не наблюдается.
 
Следует ли из данного поста, что приведенная улыбка оптимальна для использования в торговле? Ответ зависит от способа торговли. В следующей статье я выведу альтернативную улыбку, посчитанную другим способом.
 

P.S. Заинтересован в работе, связанной с опционами. Пишите в личку.