Блог им. uralpro
Алготорговля коинтегрированными активами. Часть 2
- 02 сентября 2015, 09:00
- |
Начало здесь.
Задача оптимизации инвестиций
Целью трейдера при открытии позиций в активах является максимизация ожидания имеющихся ресурсов при постоянной ревизии этих позиций в течение времени, для того, чтобы обеспечить динамическую оптимальность стратегии. Обозначим 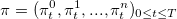 величину в денежном исчислении, инвестированную в безрисковый
величину в денежном исчислении, инвестированную в безрисковый 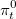 и рисковые активы
и рисковые активы 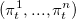 . Тогда количество открытых трейдером контрактов будет равно
. Тогда количество открытых трейдером контрактов будет равно 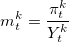 . Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:
. Опустим сложный вывод конечной формулы и представим окончательное решение в закрытой форме для доли инвестиций в активы:
![Алготорговля коинтегрированными активами. Часть 2 \pi^*=\frac{1}{\gamma}\{\mathbf{\Omega}^{-1}(\mathbf{\delta}\alpha+\mathbf{\nu})+(\mathbf{\delta}'\mathbf{\Omega}\mathbf{\delta})[\frac{1}{2}\tau(\alpha-2\frac{\mathbf{\delta'\Omega\nu}}{\mathbf{\delta'\Omega\delta}})+\frac{1}{4}Tr(\mathbf{A\Omega})\tau^2]\mathbf{a}\}](http://mathurl.com/ozsz2e9.png)
где π∗- вектор оптимальных долей в используемых активах,
τ=T−t,
γ- мера риска (подбирается при тестировании).
Первое слагаемое в приведенной формуле является классической мертоновской задачей, при том, что (δα+ν)- дрифт цен активов. Второе слагаемое, пропорциональное а, представляет собой корректировку, связанную с коинтеграцией. Как показывает это выражение, преобразования в мертоновском портфеле уменьшаются при приближении конечного времени Т. В итоге, оптимальная стратегия зависит от α, в общем случае оптимального инвестирования в несколько коинтегрированных активов.
Эмпирическая производительность стратегии
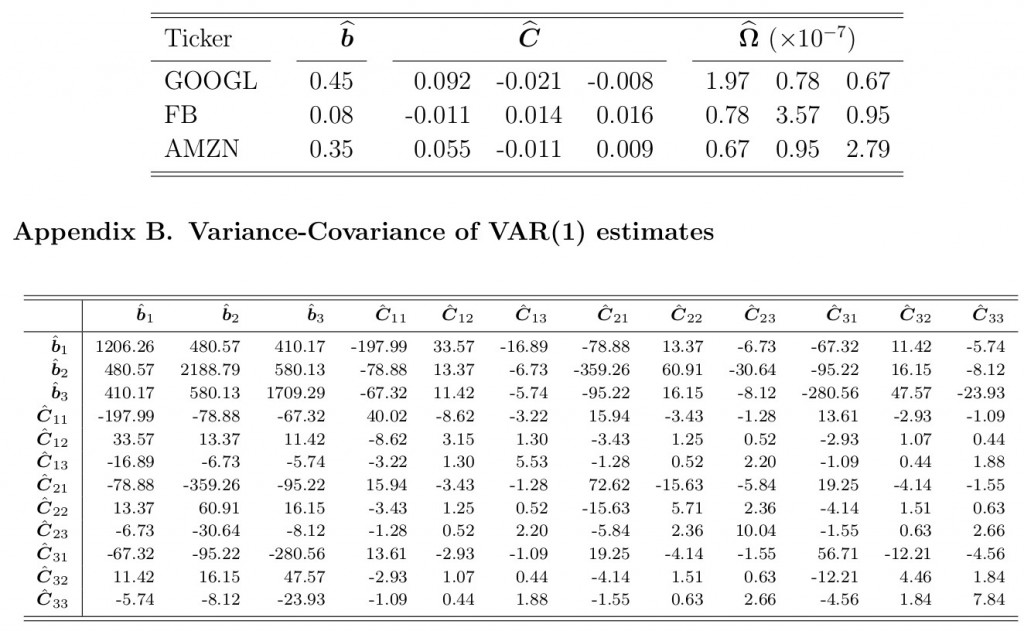
В этом разделе мы продемонстрируем поведение стратегии в случае использования трех активов. Агент торгует портфелем из трех акций — GOOGL, FB, AMAZON, и мы используем реальные данные с биржи Nasdaq для определения параметров модели. Конкретно, мы используем средние цены книги заявок с периодичностью в одну минуту от 3 ноября 2014 года, для определения параметров VAR(1) модели логарифма цен в соответствии с регрессией:
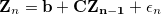
где Zn=log(Yn),ϵ1,ϵ2,...- независимые случайные переменные со стандартным нормальным распределением (с ковариационной матрицей Ω) и 3х1 вектор b, и 3х3 матрица С , установленные из множественной регрессии. Из ошибок регрессии затем составляется дисперсионно-ковариационная матрица для ϵ1. В таблицах ниже представлены результаты вычислений коэффициентов и дисперсионно-ковариационной матрицы.
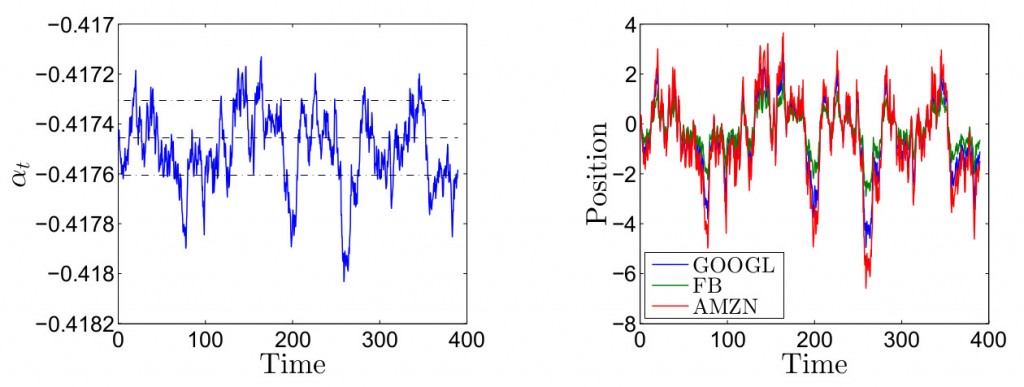
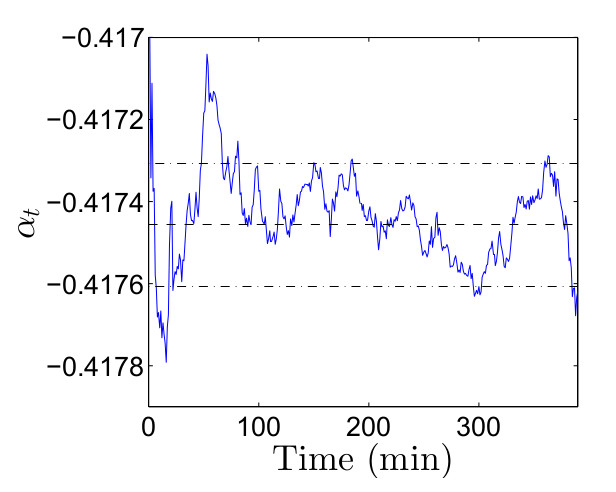
На рисунке ниже показано значение коинтеграционного фактора αt из тренировочной выборки, представляющего собой, как и ожидалось, процесс возврата к среднему. Прерывистая линия на рисунке показывает уровень возврата к среднему, плюс/минус два стандартных отклонения от коинтеграционного фактора вокруг уровня возврата к среднему (линии с точкой). Понятно, что краткосрочные отклонения от этого уровня являются основной причиной прибыльности стратегии, которую мы обсудим ниже.
Далее, уменьшим размерность задачи до случая одного коинтеграционного фактора путем следующей последовательности трансформаций:
1. Определим 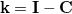 — матрица возврата к среднему, где I- единичная матрица.
— матрица возврата к среднему, где I- единичная матрица.
2. Определим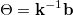 — уровень возврата к среднему
— уровень возврата к среднему
3. Диагонализируем k путем разложения 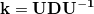 , где D — матрица собственных значений, сортированных от наибольшего к наименьшему,U — матрица собственных значений, составленных постолбцово.
, где D — матрица собственных значений, сортированных от наибольшего к наименьшему,U — матрица собственных значений, составленных постолбцово.
4. Определим матрицу с уменьшенной размерностью 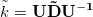 , где
, где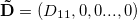 .
.
5. Затем установим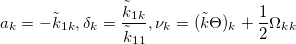 .
.
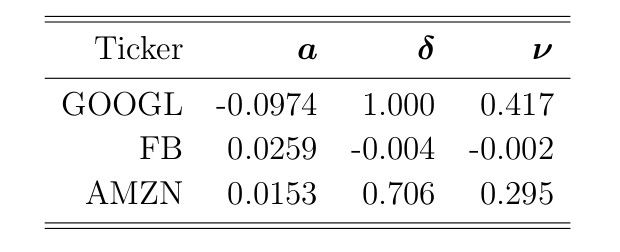
Результаты преобразований показаны в таблице ниже.
Отметим, что δ′a<0, значит процесс α, несомненно, процесс возврата к среднему.
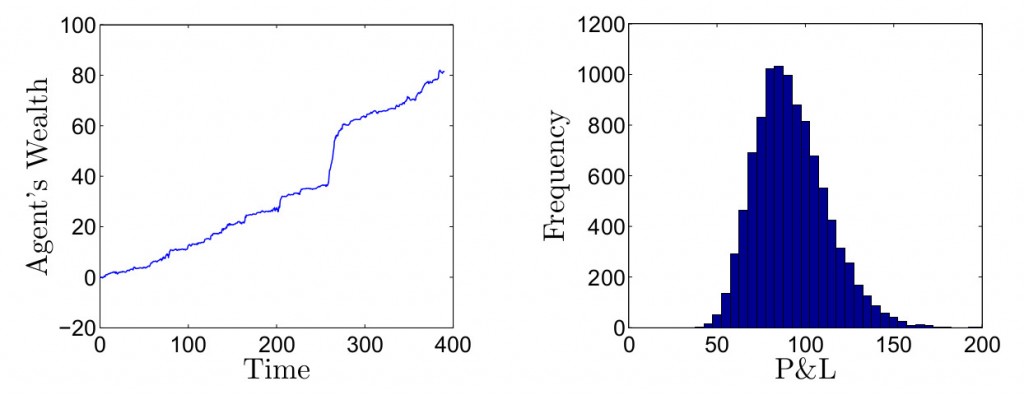
Для иллюстрации производительности стратегии мы произвели 10 000 симуляций и записали профиль P&L в каждом случае. Мы использовали установленные выше параметры для симуляции компонента краткосрочной альфы и графика коинтеграционной цены (для каждой минуты внутри торгового горизонта) для Google, Facebook и Amazon. Для каждого прохода мы предполагали, что агент начинает с нулевыми открытыми позициями в активах и все позиции ликвидируются в конце дня, все транзакции происходят по средней цене книги заявок и нет транзакционных издержек. На графиках в заглавии поста показан один из симуляционных путей αt и соответствующие ему оптимальные позиции в активах. На графиках ниже изображен процесс изменения ресурсов агента для данного пути и гистограмма прибыли/убытков для 10 000 проходов. Среднее значение прибыли составляет 91,99 и стандартное отклонение прибыли 20,27.
Для данного конкретного прохода мы видим, что открытые позиции агента всегда находятся между 4 длинными и 6 короткими контрактами и прибыль в конце торгового периода составила приблизительно 80$. Открытые позиции активов демонстрируют паттерн, похожий на краткосрочную альфа прохода, оба показаны в заглавии поста. Помните, что αt включает дрифт каждого актива, так что во время, когда альфа выше уровня возврата к среднему соответствует моменту, где есть ожидание быстрого роста средних цен, то есть оптимальная стратегия — покупка актива.Соответственно, когда αt ниже уровня возрата к среднему — ожидание медленного роста цен (или даже их падения), где оптимально входить в короткие позиции по активам для получения краткосрочной прибыли от их снижения.
Заключение
Мы показали процесс оптимальной торговли набором коинтегрированных активов. Мы смоделировали структурную зависимость через общий компонент и дрифт приращений цен активов. Этот общий компонент является коинтеграционным фактором, который мы назвали краткосрочной альфа, и он является основным источником прибыльности в оптимальной инвестиционной стратегии.
Другие стратегии, алгоритмы и программы автоматического трейдинга смотрите на моем сайте — www.quantalgos.ru
теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R



















Очень познавательно.
Говорите на человеческом языке, а не на птичьем (конечно, если хотите что бы вас поняли). И вообще, будьте проще, и народ к вам потянется.
А про цели трейдера при открытии позиции можно сказать без всяких «пи»: цель срубить деньжат за счёт других участников торгов.
Правда бывают ещё цели «впарить» обучение, бота, сигналы и прочий шлак.
1. Вопрос к коинтеграции. А зачем совместная регрессия? есть ли преимущество по отношению к отдельным регрессиям? есть ли преимущество по отношению к регрессии на себя и на индекс?
2. Из поста я не понял, как из альфы, веги и дельты получить цены акций.
Товарищ uralpro, мне два заверните на вынос!
2. В общем-то вся статья и есть о преимуществе совместной регрессии. Суть в выделении общего компонента, который отражает совместную коинтеграцию активов на основе общего фактора. Понятно, что в отдельных регрессиях этот компонент будет смешан с другими факторами, которые присущи только двум взятым активам.
3. А зачем вам цены? Вы же торгуете спред, вам нужно только знать коэффициенты для каждого актива, которые вы легко вычислите из первого уравнения
U — матрица не из собственных значений, а из собственных векторов. Но есть непонятка, Вы рассуждаете так, словно С — самосопряженная матрица. А это не так.
Если там попарные коэфф. ковариации, то должна быть симметричной, конечно. Но в табличке омега симметричная, а С — нет.
Или что-то я неправильно понимаю.
это уже постфактум-оптимизация, т.е. подгон под случившееся событие, а это лишено всякого смысла
так, пощекотать самолюбие красивой картинкой «как могло бы быть» )))
Еще раз перечитал и понял, что в первый раз подкорочно осталось:
"γ- мера риска (подбирается при тестировании)". То есть имеете волатильность бумажки, определяете меру риска ПО РЕЗУЛЬТАТАМ ТЕСТИРОВАНИЯ, а затем меру риска при котором пОртфель показывает плюс подставляете для будущих сделок.
Ребята, которые получили Нобеля за оценку портфелей, слились в один момент. Их просто не стало. И, да, они тоже считали меру риска и собственный слив оценивали как 1 раз в 10.000 лет. И вот надо ж, случилось прям сразу! ))))