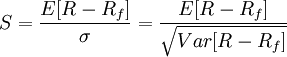Коэффициент Шарпа, как и альфа, оценивает труд управляющего. Только сравнивает доходность портфеля не с движением какого-либо эталона, а с колебанием доходности самого портфеля за анализируемый период. Т.е. дается «внутренняя» оценка «качества» доходности портфеля, без использования «внешних» данных. Другими словами, дается абсолютная, а не относительная оценка полученной за период доходности.
, где
• R — доходность портфеля (актива)
• Rf — доходность от альтернативного вложения
• σ — стандартное отклонение доходности портфеля (актива)
Колебания доходности — это риск. Высокие колебания — это высокий риск, и они должны приносить высокий доход. Колебания доходности измеряются стандартным отклонением, которое помещается в знаменатель дроби, рассчитывающей коэффициент Шарпа. В числителе дроби – доходность портфеля, очищенная от гарантированной рыночной доходности — от доходности безрискового вложения, в качестве которого, как правило, берется депозит в Сбербанке.
Если портфель показал доходность 30% со стандартным отклонением равным 10, а депозит Сбербанка принес бы 12%, то коэффициент Шарпа будет равен (30-12)/10 = 1,8. Можно сказать, что за каждую единицу риска были получены 1,8 единиц доходности сверх гарантированной безрисковой доходности.
Чем значение коэффициента Шарпа выше, тем выгоднее управляющий использует риск портфеля. Причем, благодаря тому, что этот коэффициент использует стандартное отклонение доходности самого портфеля, а не внешний эталон, он может быть применен для сравнения между собой различный портфелей.
При одинаковой доходности портфели могут иметь разные значения этого коэффициента, потому что они принимают на себя разное количество риска. Портфель, у которого коэффициент Шарпа выше при одинаковой доходности, достиг результата с меньшим риском. Чем выше стандартное отклонение, тем больше знаменатель уравнения коэффициента Шарпа, а значит портфелю нужно показывать высокую доходность, чтобы заработать высокое значение этого показателя. Портфелю с низким уровнем риска (небольшим стандартным отклонением) достаточно показывать умеренную доходность, чтобы его коэффициент Шарпа был достаточно высоким.
У коэффициента Шарпа есть преимущество перед альфой. Стандартное отклонение измеряет волатильность фонда в абсолютной величине, а не относительной, как альфа. Поэтому, если для полезности альфы должен быть высоким коэффициент корреляции, то коэффициент Шарпа всегда имеет полноценное значение, независимо от других показателей.
