SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. hannimed |Оптимальный интервал для рехеджа портфеля
- 17 января 2020, 01:44
- |
Небольшое отступление. После предыдущих постов, я получал сообщения в личку, о том, что не все было понятно. Я постараюсь писать более понятным для новичков языком, и опытных коллег прошу простить чрезмерную избыточность материала в некоторых местах. Я буду рад любым замечаниям и уточнениям. В конечном счете, цель данного поста, закрепить и самому разобраться в тонкостях этой темы.
В данной статье мы попробуем разобраться, как влияет дискретность хеджирования и стоимость транзакций на дельта-хеджирование (ДХ). О том, что такое ДХ и механизм его работы, можно прочитать в моих предыдущих постах или любых других постах, но лучше всего в книгах.
ДХ по Блэку-Шоулзу (БШ), предполагает непрерывное хеджирование. Это означает, что ребалансировка портфеля должна происходить на бесконечно малых промежутках времени. И именно в таких условиях, ДХ по БШ обеспечивает хеджирование портфеля в полной мере, т.е. позволяет свести риски убытков к минимуму.
( Читать дальше )
В данной статье мы попробуем разобраться, как влияет дискретность хеджирования и стоимость транзакций на дельта-хеджирование (ДХ). О том, что такое ДХ и механизм его работы, можно прочитать в моих предыдущих постах или любых других постах, но лучше всего в книгах.
ДХ по Блэку-Шоулзу (БШ), предполагает непрерывное хеджирование. Это означает, что ребалансировка портфеля должна происходить на бесконечно малых промежутках времени. И именно в таких условиях, ДХ по БШ обеспечивает хеджирование портфеля в полной мере, т.е. позволяет свести риски убытков к минимуму.
( Читать дальше )
- комментировать
- ★15
- Комментарии ( 61 )
Блог им. hannimed |Механизм работы дельта-хеджирования для новичков
- 18 июня 2019, 11:22
- |
Есть мнение, чтобы хорошо что-то освоить, нужно кого-нибудь этому научить. В целях самообразования и, возможно, ради чьей-нибудь пользы, попробуем разобраться, что же такое дельта-хеджирование. Эта статья основана на двух предыдущих, в которых освещались основы языка R и объяснялось, что такое паритет опционов.
Откуда берется дельта?
Давайте представим, что у нас есть следующая позиция:
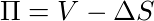
( Читать дальше )
Откуда берется дельта?
Давайте представим, что у нас есть следующая позиция: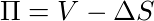
- П — портфель или портфолио, кому как больше нравится
- V — стоимость опциона
- ΔS — стоимость базового актива
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- анализ
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- ецб
- золото
- инвестиции
- инфляция
- китай
- коронавирус
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опек+
- опрос
- опционы
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- финансы
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- шорт
- экономика
- юмор
- яндекс



















