Beta vs Delta

На прошедшей 18 мая конференции НОК-6 я сделал доклад, часть которого была посвящена способам вычисления дельты. Ссылка на презентацию есть в моем предыдущем посте: http://quant-lab.com/events/poc-6.html



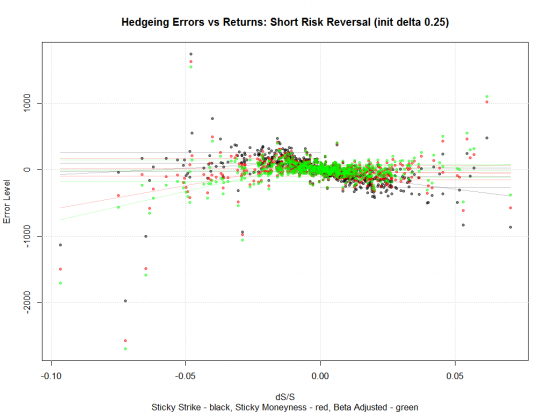
Сейчас я хочу рассказать о методе расчета дельты (я его назвал Beta Adjusted). Повторюсь, что в своем докладе я рассмотрел два метода для вычисления дельты опциона — Sticky Strike и Sticky Moneyness. Третий метод Beta Adjusted — это модифицированный мной Sticky Moneyness. Но обо всем по порядку.

Hedge setup

Для оценки точности вычисления дельты тем или иным способом я использовал анализ ошибок хеджирования. Хеджировались следующие портфели: короткий пут, короткий колл, короткий стрэнгл, риск-реверсал (дельты опционов, составляющих портфели, были по модулю равны 0.5, 0.25, 0.1 и 0.05). Портфель открывается по теоретическим ценам на конец рассматриваемого торгового дня. Далее вычисляется дельта одним из указанных способов, и в портфель добавляется позиция по базовому активу, нейтрализующая дельту, по расчетной цене на момент закрытия торгов. На следующий торговый день позиция закрывается также по теоретическим ценам. Ошибка хеджирования определяется как финансовый результат, к которому приводят данные операции, за вычетом однодневной теты портфеля (если тета отрицательная, то фактически ее модуль добавляется к результату). Были рассчитаны ошибки хеджирования за период с 2010-03-01 по 2013-04-30 для опционов, до экспирации которых оставалось от 30 до 5 календарных дней включительно.


Hedging Errors vs log-Returns

Приведу несколько графиков с ошибками хеджирования (ось Y) и соответствующими им изменениями цен базового актива (ось X), в презентации приводится большее количество графиков:


Если посмотреть на результаты (ошибки) дельта-хеджирования, получаемые при использовании методов Sticky Strike (черные точки) и Sticky Moneyness (красные), видно что ошибки располагаются несимметрично. Это означает, что фактически дельта не была нейтральна. Особенно это заметно для портфеля риск-реверсал. При нейтрализации его дельты методом «липкого страйка» мы фактически получали портфель с отрицательной дельтой. Безусловно такие результаты нас не радуют.

Beta Adjusted

Попробуем улучшить метод Sticky Moneyness, добавив к нему возможность учитывать так называемый эффект левериджа, когда волатильность возрастает с падением цены базового актива и, наоборот, снижается при ее росте. Чтобы реализовать это, мы должны знать на сколько увеличиться/уменьшится implyed volatility опциона с заданным уровнем дельты при движении базового актива на единицу его цены. Сделать это можно аналогично методике, описанной в данном посте http://quant-lab.com/research/returns-vs-volatility.html
На рисунках ниже приводятся графики зависимости коэффициента бета от начальной дельты опциона:

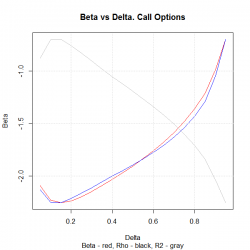
Стоит отметить, что согласно нашим расчетам волатильность ОТМ опционов колл острее реагирует на возмущения цен базового актива, чем волатильность ITM. И, наоборот,  зависимость implyed volatility опционов пут от возмущений БА больше в зоне ITM, чем в OTM. Зная коэффициент бета для опциона с любой дельтой, мы можем добавить влияние эффекта левериджа в формулу для расчета дельты по методу Sticky Moneyness (формула приводится в презентации).
Получим следующие ошибки хеджирования (Beta Adjusted выделены зеленым):


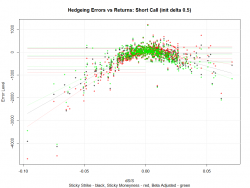
Заключение

Мы получили более симметричное взаимное расположение ошибок (баланс кумулятивных сумм ошибок для отрицательных и положительных возмущений цен БА улучшился на 62% по сравнению с методом Sticky Strike). Кроме этого стандартное отклонение также улучшилось (на 7% по сравнению с методом Sticky Strike). Это дает нам повод считать новый метод Beta Adjusted более точным для вычисления дельты отдельных опционов и портфелей.

Анонс следующей статьи

Объектом моих последующих исследований станут Risk Reversal и Butterfy как показатели «ассимметрии» и «куртозиса» улыбки волатильности.
Также я планирую написать небольшую статью о методе Vanna-Volga.

В полном объеме статься находится:
http://quant-lab.com/research/beta-vs-delta.html