Долларовая Дюрация
Дюрация Фишера-Вейла — оценка чувствительность текущей стоимости потока платежей (классической облигации или портфеля дисконтных и(или) классических облигаций), с учетом дисбаланса «спот-ставка – срок», к параллельному сдвигу функции, описывающей таковой дисбаланс.
Долларовой выпуклостью называют «чувствительность» Долларовой Дюрации к параллельному «сдвигу» кривой спот-ставок. Математически, это будет отношение производной второго порядка текущей стоимости потока платежей по «сдвигу» кривой спот-ставок к текущей стоимости потока.
_______________________________________________
На практике, рынок облигаций имеет четкую временную структуру, что не учитывалось в описываемых выше моделях*(3). Предположим, что зависимость спот-ставок*(4), или иначе, рыночных ставок процента, описывается функцией:
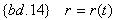
Тогда, имея сроки выплат по i-тому платежу, на основании можно {bd.14} определить соответствующую спот-ставку:
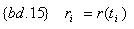
Рассмотрим, как изменится стоимость портфеля при параллельном сдвиге кривой доходности h. Чистая приведенная стоимость портфеля при параллельном сдвиге h будет равна:
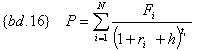
Если «сдвинутая» кривая доходности совпадает с исходной, то h равно «нулю». При малых «сдвигах» h, в точке h, равное «нулю», текущая стоимость потока платежей приблизительно изменится согласно {bd.17}:
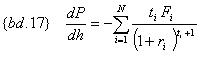
Или, введя дополнительные обозначения (w i-тое – доля приведенной стоимости соответствующего платежа в текущей стоимости потока):
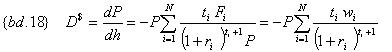
Полученная производная {bd.18} носит название долларовой Дюрации Фишера-Вейла и позволяет оценивать чувствительность текущей стоимости потока платежей (классической облигации или портфеля дисконтных и(или) классических облигаций), с учетом дисбаланса «спот-ставка – срок», к параллельному сдвигу функции, описывающей таковой дисбаланс.
Долларовой выпуклостью называют «чувствительность» Долларовой Дюрации к параллельному «сдвигу» кривой спот-ставок. Математически, это будет отношение производной второго порядка текущей стоимости потока платежей по «сдвигу» кривой спот-ставок к текущей стоимости потока:

Существуют и другие меры чувствительности текущей стоимости потока платежей к более сложным видам деформаций кривой доходности [см. например, 4].
Однако следует обратить внимание на следующий любопытный факт: согласно исследованию факторов, «сдвигающих» и «деформирующих» зависимость доходности от срока [4] на американском рынке инструментов с фиксированной доходностью, 95% волатильности кривой доходности обусловлено параллельными сдвигами. Второй фактор объясняет 2% общей волатильности кривой доходности, он влияет на крутизну кривой доходности. Третий фактор объясняет около 1% волатильности, и влияет на кривизну кривой доходности в краткосрочном периоде. Полученные результаты являются общими для всех рассматриваемых сегментов рынка облигаций, которые определяются кредитным рейтингом заемщика.
Подобному анализу был подвергнут и российский рынок ГКО/ОФЗ [1]. И согласно исследованиям, главным фактором изменения кривой доходности рынка Российских госбумаг также является параллельный сдвиг.
______________________________________________________
*(1) в [2 стр. 456] со ссылкой на [3] данные утверждения приводятся как «теоремы, связанные с оценкой облигаций.
*(2) SIA (Securities Industry Association) Semi-Annual Yield Conventions [6].
*(3) точнее следует заявить, что при изложенном подходе отсутствовало деление облигаций по группам, в зависимости от срока до погашения. А именно, отсутствовал дисбаланс по показателю «доходность–срок обращения». Надо заметить, что подобное крайне редко наблюдается в действительности. С другой стороны, изложение моделей и примеров приводилось не с использованием рыночных процентных ставок, а на основании одной единственной ставки, соответствующей ставке доходности к погашению для рассматриваемых инструментов. Источник данных для расчетов и анализа [yaha]
*(4) спот-ставка (spot rate) – доходность к погашению в годовом исчислении дисконтной ценной бумаги [2 стр. 119 или 993].
Литература:
1.Ливингстон Г. Дуглас. Анализ рисков операций с облигациями на рынке ценных бумаг. М: Информационно-издательский дом «Филинъ», 1998.
2.Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М: ИНФРА-М, 2001. – XII, 1028 с.
3.Burton J. Makliel, “Expectation, Bond prices, and the Term Structure of Interest Rates”, Quarterly of Economics, 76, no 2 (may 1962), pp. 197-218.
4.Bertocchi M., Giancometti R., Zenios S. Risk factor analysis and portfolio immunization in the corporate bond market. 2000, November 2.
5.Fabozzi, Frank J., and T. Dessa Fabozzi, eds. The Handbook of Fixed-Income Securities. Burr Ridge, IL: Irwin. 4th ed., 1995, ISBN 0-7863-0001-9.
6. Mayle, Jan. Standard Securities Calculation Methods. New York: Securities Industry Association, Inc. Vol. 1, 3rd ed., 1993, ISBN 1-882936-01-9. Vol. 2, 1994.
7.Principles for the Management and Supervision of Interest Rate Risk. Basel Committee on banking Supervision. 2001. January. Материалы сайта http://www.bis.org/
Документация к ПО:
8.MATLAB: Financial toolbox documentation — Pricing and Computing Yields for Fixed-Income Securities// Mathworks Software http://www.mathworks.com/
Интернет ресурсы:
9.Bonds Screener //Материалы сайта http://www.finance.yahoo.com/
Долларовой выпуклостью называют «чувствительность» Долларовой Дюрации к параллельному «сдвигу» кривой спот-ставок. Математически, это будет отношение производной второго порядка текущей стоимости потока платежей по «сдвигу» кривой спот-ставок к текущей стоимости потока.
_______________________________________________
На практике, рынок облигаций имеет четкую временную структуру, что не учитывалось в описываемых выше моделях*(3). Предположим, что зависимость спот-ставок*(4), или иначе, рыночных ставок процента, описывается функцией:
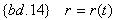
Тогда, имея сроки выплат по i-тому платежу, на основании можно {bd.14} определить соответствующую спот-ставку:
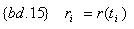
Рассмотрим, как изменится стоимость портфеля при параллельном сдвиге кривой доходности h. Чистая приведенная стоимость портфеля при параллельном сдвиге h будет равна:
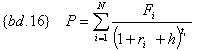
Если «сдвинутая» кривая доходности совпадает с исходной, то h равно «нулю». При малых «сдвигах» h, в точке h, равное «нулю», текущая стоимость потока платежей приблизительно изменится согласно {bd.17}:
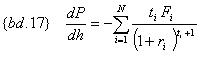
Или, введя дополнительные обозначения (w i-тое – доля приведенной стоимости соответствующего платежа в текущей стоимости потока):
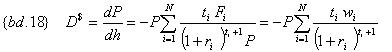
Полученная производная {bd.18} носит название долларовой Дюрации Фишера-Вейла и позволяет оценивать чувствительность текущей стоимости потока платежей (классической облигации или портфеля дисконтных и(или) классических облигаций), с учетом дисбаланса «спот-ставка – срок», к параллельному сдвигу функции, описывающей таковой дисбаланс.
Долларовой выпуклостью называют «чувствительность» Долларовой Дюрации к параллельному «сдвигу» кривой спот-ставок. Математически, это будет отношение производной второго порядка текущей стоимости потока платежей по «сдвигу» кривой спот-ставок к текущей стоимости потока:

Существуют и другие меры чувствительности текущей стоимости потока платежей к более сложным видам деформаций кривой доходности [см. например, 4].
Однако следует обратить внимание на следующий любопытный факт: согласно исследованию факторов, «сдвигающих» и «деформирующих» зависимость доходности от срока [4] на американском рынке инструментов с фиксированной доходностью, 95% волатильности кривой доходности обусловлено параллельными сдвигами. Второй фактор объясняет 2% общей волатильности кривой доходности, он влияет на крутизну кривой доходности. Третий фактор объясняет около 1% волатильности, и влияет на кривизну кривой доходности в краткосрочном периоде. Полученные результаты являются общими для всех рассматриваемых сегментов рынка облигаций, которые определяются кредитным рейтингом заемщика.
Подобному анализу был подвергнут и российский рынок ГКО/ОФЗ [1]. И согласно исследованиям, главным фактором изменения кривой доходности рынка Российских госбумаг также является параллельный сдвиг.
______________________________________________________
*(1) в [2 стр. 456] со ссылкой на [3] данные утверждения приводятся как «теоремы, связанные с оценкой облигаций.
*(2) SIA (Securities Industry Association) Semi-Annual Yield Conventions [6].
*(3) точнее следует заявить, что при изложенном подходе отсутствовало деление облигаций по группам, в зависимости от срока до погашения. А именно, отсутствовал дисбаланс по показателю «доходность–срок обращения». Надо заметить, что подобное крайне редко наблюдается в действительности. С другой стороны, изложение моделей и примеров приводилось не с использованием рыночных процентных ставок, а на основании одной единственной ставки, соответствующей ставке доходности к погашению для рассматриваемых инструментов. Источник данных для расчетов и анализа [yaha]
*(4) спот-ставка (spot rate) – доходность к погашению в годовом исчислении дисконтной ценной бумаги [2 стр. 119 или 993].
Литература:
1.Ливингстон Г. Дуглас. Анализ рисков операций с облигациями на рынке ценных бумаг. М: Информационно-издательский дом «Филинъ», 1998.
2.Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М: ИНФРА-М, 2001. – XII, 1028 с.
3.Burton J. Makliel, “Expectation, Bond prices, and the Term Structure of Interest Rates”, Quarterly of Economics, 76, no 2 (may 1962), pp. 197-218.
4.Bertocchi M., Giancometti R., Zenios S. Risk factor analysis and portfolio immunization in the corporate bond market. 2000, November 2.
5.Fabozzi, Frank J., and T. Dessa Fabozzi, eds. The Handbook of Fixed-Income Securities. Burr Ridge, IL: Irwin. 4th ed., 1995, ISBN 0-7863-0001-9.
6. Mayle, Jan. Standard Securities Calculation Methods. New York: Securities Industry Association, Inc. Vol. 1, 3rd ed., 1993, ISBN 1-882936-01-9. Vol. 2, 1994.
7.Principles for the Management and Supervision of Interest Rate Risk. Basel Committee on banking Supervision. 2001. January. Материалы сайта http://www.bis.org/
Документация к ПО:
8.MATLAB: Financial toolbox documentation — Pricing and Computing Yields for Fixed-Income Securities// Mathworks Software http://www.mathworks.com/
Интернет ресурсы:
9.Bonds Screener //Материалы сайта http://www.finance.yahoo.com/
Связанные статьи:
- 7 +6 11/07 Дюрация
- 2 +15 11/07 Дюрация облигации
- +5 15/11 Дисконтные облигации
- 06/05 катастрофические облигации
- 1 21/04 замещающие облигации
- 23/07 дефолты по российским облигациям

















