Блог им. Gusan
Точность прогноза
- 27 июня 2015, 01:17
- |
Допустим, есть две системы, которые выдают прогноз — где будет БА на экспирацию. Прогноз выдается в виде распределения вероятностей. Задача: оценить на истории — какая система выдает более точный прогноз.
Вот картинка для иллюстрации. Слева график цены БА, справа два графика плотности вероятности, синий для распределения P, зеленый для распределения Q. Красным кружочком отмечен уровень S, где реально оказалась прогнозируемая цена:
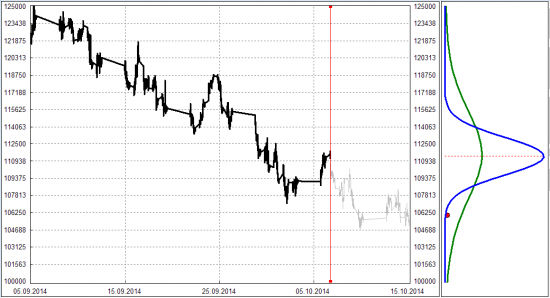
Для оценки точности прогноза пробовал считать средний квадрат отклонения распределения от S (кажется, этот метод называется MSE). Для вышеприведенной картинки такое отклонение меньше у распределения P. Но, мне кажется, что распределение Q более точное: оно дает гораздо большую вероятность для красного кружочка.
Может кто подскажет — можно ли как-то по другому считать точность распределения-прогноза?



















Что Вы имели ввиду под фактическим распределением?
Если да, то тут есть большие сомнения. Получается, из прошлого можно извлечь распределение, которое будет предсказывать будущее. И это распределение будет самым правильным.
Мне ближе точка зрения, что историческая траектория цены — лишь одна из бесконечного кол-ва возможных. И по одной этой траектории невозможно восстановить истинное распределение вероятностей.
Для док-ва рассмотрим обратную задачу: допустим у нас есть случайный процесс, который хорошо описывает рынок, в нем есть случайное блуждание с переменной волатильностью, с гэпами, с всплесками волы и возвратом к средней воле, вола волы (что-то вроде модели Хестона + гэпы). С его помощью мы можем сгенерить миллион разных траекторий цены и получить истинное (для нашего процесса) распределение на экспу D. Теперь берем только одну из сгенерированных траекторий. Разве мы сможем по ней одной восстановить распределение D?
-Разве мы сможем по ней одной восстановить распределение D?
Это надо курить бутстреппинг:)) кстати, наверно несложно проверить: вначале генерируете по выбранной модели одну траекторию, а потом из неё бутстрепом пытаетесь восстановить первоначальную модель.
Мне кажется, правильный путь — это все выявленные закономерности и предположения оформить в виде модели, выдающую распределение. Потом на истории посчитать насколько ошибалась эта модель. И сравнить с ошибкой рыночного распределения (которое получается из биржевой улыбки). Если удастся найти такую модель, чтобы более-менее устойчиво выдавала меньшую ошибку чем рынок, то вот и грааль :)
Если заблуждаюсь — прошу поправить.
Сам близко капаю)) Но я сравниваю только модели волатильности и вот думаю как раз над тем как сравнить с улыбкой или виксом из прогнозную силу.
Насчет другой серии — мне кажется, это другая совершенно задача. Арбитраж между календарными сериями — тема интересная, но никак не связана с обсуждаемой. Брать из обоих серий два распределения, нормировать их на оставшееся время до экспы, и получить таким образом усредненное — может быть неправильным. Например, допустим ожидает рынок что в августе может быть сильный гэп, и поэтому M4 (этот момент отвечает за толстые хвосты) у сентябрьской серии будет больше чем у июльской (а значит и IV на центре сентября будет выше IV на центре июля). И это будет справедливо. А брать и насильно повышать M4 июльской серии, в такой ситуации будет неправильным, имхо.
когда мы берём две улыбки то не надо их нормировать на срок до экспирации можно просто брать фиксированное время, например 22 дня, а потом переводить это в однодневное распределение чтобы сравнить с рыночным распределением.
У вас цена актива — случайная величина — кумулятивная сумма случайных пошаговых приращений цены. То, что в конечный момент времени цена оказалась равна S — тоже случайность — «одна из бесконечного количества траекторий». Вы не знаете, равно ли S матожиданию цены, или оно за 2-3 сигмы выходит. Оценивать по одному случайному значению S правильность ваших моделей как-то неправильно.
Для того, чтобы восстановить по одной траектории распределение, как раз и используют bootstrapping.
Это относительно какого распределения? Некоего самого точного и правильного? Имхо, такого нет и задачи найти такое себе не ставлю. Нужно просто найти такую модель, которая ошибалась бы меньше чем рынок (распределение из биржевой улыбки). Т.е., грубо говоря, пусть модель ошиблась на 2-3 сигмы, но если рынок при этом ошибся на 4-5 сигмы, то значит модель оказалась точнее. И если удастся найти такую, чтобы устойчиво была точнее рынка, то дальше уже дело техники.
Оценивать собираюсь на каждом баре и потом считаю среднюю ошибку: вот график ошибок (нижний). И это только одна месячная серия, а есть шестилетняя история.
Можно ли на основании полученного распределения что-то прогнозировать — не факт, т.к. система у нас скорее всего нестационарная.
Пусть распределением D мы прогнозируем в момент времени T1 где будет цена S на экспу (момент времени T2). В момент прогноза (T1) S будет случайной величиной (поскольку ее нельзя 100% точно предсказать). Но в момент T2 S будет уже 100% точно известной величиной. Т.е. в момент когда считаем насколько точным оказалось распределение D — величину S уже нельзя считать случайной. Имхо.
en.wikipedia.org/wiki/Likelihood-ratio_test
фактическое это реальные данные ваши. сравнивается для какого из двух ваших систем они более правдоподобны, т.е. более вероятны.
Все эти критерии есть в R — можно гуглить сразу с примерами, но это лучше на английском делать.
Можно было бы считать ошибку как разницу между МО распределения и S. Но в такой оценке получается участвует только первый момент, а нужно учитывать еще как минимум второй (дисперсию). Если получится учитывать третий и четвертый — было бы совсем замечательно.
Вообще точность системы прогнозирования на единственном испытании оценить невозможно. Нужна серия испытаний.
1. Более точный прогноз должен показывать большую вероятность для цены S. Если распределение P давало вероятность 0.1%, что цена снизиться ниже S, а распределение Q давало вероятность 10%, то Q оказалось точнее.
2. Если оба распределения показывают примерно одинаковую вер-ть для S, то более точным можно считать то, у которого дисперсия меньше.
Насчет серии испытаний — так и делаю. Считаю ошибку на каждом баре, нормирую на Sqrt(T) и потом считаю среднюю. Вот график ошибок (нижний).
Спасибо, что натолкнули на эту мысль.
если по критерию близости (прогнозной силе) к реальному значению (на тестовых выборках),
то основных способов 3 (хотя их много, и т.к. здесь ряд, то возможно нужен MASE):
1. средняя квадратичная ошибка (это Вы сделали)
2. средняя ошибка по модулю
3. средняя процентная ошибка
Как мне кажется для цен лучше считать по 3 способу (или по MASE),
но можно считать по всем 3-4 и думать дальше.
Если просто выбирать модель, то можно попробовать смотреть на критерий Фишера и/или на информационные критерии AIC, BIC и т.д.,
но это только в том случае, если в модели есть функция правдоподия, но и то это не совсем корректно для выбора лучшей модели.
Но, после коммента Spekyl, сделал другой вариант. Поскольку в конечном счете интересует не абстрактная оценка произвольного распределения, а насколько лучше/хуже моя модель (распределение P) относительно рынка (распределение Q). Поэтому в качестве оценки взял просто разность P-Q в точке S. И пока такая оценка мне нравится больше всего. Для плохой модели она дает плохую оценку. Для заведомо хорошей (заглядываю в «будущее») — устойчиво хорошую. Так что, скорее всего именно эту оценку буду использовать.
en.wikipedia.org/wiki/Mean_absolute_scaled_error