SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. broker25
Толстые хвосты и эмпирические распределения
- 06 июня 2013, 15:15
- |
Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра.
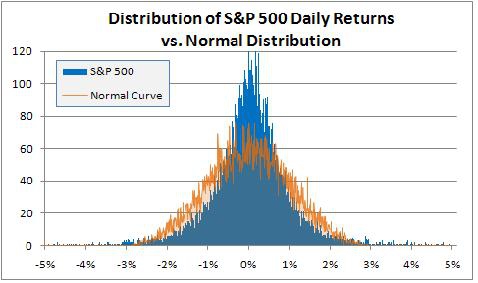
Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже
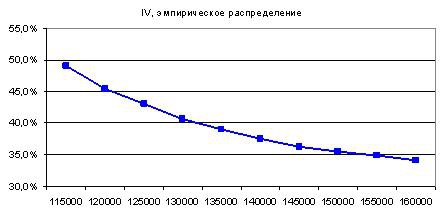
Откуда, по вашему мнению, на графике выше появилась улыбка? Из-за толстых хвостов! – наверняка скажут многие. Тогда, спрошу я, откуда же берется улыбка на рисунке ниже?
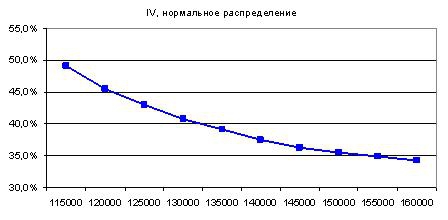
График построен не по эмпирическому распределению, а по нормальному, но с теми же параметрами, как и эмпирическое (матожидание и среднекв. отклонение). Параметры рассчитаны для нашего ряда логарифмов. Конечная цена фьючерса для эмпирического распределения определяется по формуле
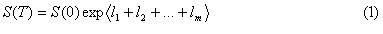
где li –логарифм Ln( S(i)/S (i-1)), случайно выбранный из нашего ряда.Для нормального распределения меняем li на ni
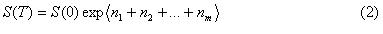
где ni – нормальная величина (0; ср.отклонение ряда li.)
Откуда же взялась улыбка там, где ее не должно быть?
Ответ в том, что, хотя нам казалось, что по построению мы исключили тренд, на самом деле положительный тренд возник. Ведь если цена непрерывно движется по броуновскому закону, как предполагается в модели БШ,

то c течением времени у логарифма цены возникает тренд

То есть, матожидание Ln(S(T)) – Ln(S(0)) равно (4). А у нас, напомню, эмпирическое распределение выбрано из ряда, в котором начальная и конечная цены совпадают, и, как следствие, матожидание Ln(S(T)) – Ln(S(0)) равно нулю . Таким образом, в нашем опыте с точки зрения модели БШ актив движется с положительным трендом µ, равным σ* σ /2 (T-t). Тренд повлиял на стоимость опционов колл, причем прирост стоимости опционов дальних страйков из-за тренда оказался не менее сильным (а по факту даже большим), чем для ближних. Искажение цен опционов привело к возникновению улыбки.
Замечу, что сам расчет цены опционов и их волатильности был некорректен. Если существует тренд, отличный от безрисковой ставки (которая для фьючерсов равна нулю), то инвестор не нейтрален к риску, ведь для риск-нейтрального инвестора все активы приносят один доход, равный безрисковой ставке. Если инвестор не риск-нейтрален, то считать стоимость опциона методом усреднения модельных терминальных цен нельзя, т.к. такой инвестор оценивает ценность прибыли и убытка по-разному. Внесем коррекцию, добавим тренд -σ* σ /2 (T-t) к эмпирическому и нормальному распределениям и нарисуем соответствующие улыбки
Мы видим, что отличия в улыбках минимальны. Они объясняются случайной ошибкой в рамках модели. Волатильность слева более чувствительна к ошибкам, поэтому размах колебаний выше. Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки на данном временном интервале. Замечу, что и в случае нескорректированной на тренд модели, отличия между двумя улыбками также минимальны и объясняются случайными ошибками.
Любопытно, что аналогичные выводы получаются, если использовать не эмпирическое, а другое распределение цен с толстыми хвостами, имеющее конечную дисперсию и матожидание. В частности, похожий опыт был когда-то поставлен мной для распределения Пирсона седьмого порядка с куртозисом, взятым из рыночного распределения. В этом случае улыбка также вырождается в прямую линию.
Причина отсутствия улыбки – Центральная Предельная Теорема, смысл которой состоит в том, что сумма независимых, одинаково распределенных случайных величин стремится в пределе к нормальному распределению. В нашем случае сумма величин li в формуле (1) дает величину, близкую к нормальной, в связи с большим периодом модели, равным ста шагам. Вопрос о меньшем количестве шагов модели будет рассмотрен в другой статье.
Эмпирическое распределение может быть построено и для приращений актива, которые не являются независимыми. В частности, в журнале ФиО n1-2 за 2009г. Израйлевичем и Цудикманом была представлена модель оценки опционов на основе доходности актива за периоды, равные времени до экспирации. Однако, применяя рассуждения, аналогичные изложенным выше, мы убедимся, что использование исторических рядов цен в общем случае приведет к возникновению тренда и искажению стоимости опционов в модели. Для более точной оценки модель должна быть скорректирована на тренд.
Выводы:
1. Эмпирическое распределение для оценки стоимости опционов следует применять с коррекцией на тренд.
2. В модели ежедневных независимых приращений цен актива, построенной на основе исторических данных, улыбки волатильности не возникает при сроках до экспирации выше 100 дней.
Ссылки
график ежедневных доходностей S&P 500 взят с сайта
http://managed-futures-blog.attaincapital.com/

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

Откуда, по вашему мнению, на графике выше появилась улыбка? Из-за толстых хвостов! – наверняка скажут многие. Тогда, спрошу я, откуда же берется улыбка на рисунке ниже?

График построен не по эмпирическому распределению, а по нормальному, но с теми же параметрами, как и эмпирическое (матожидание и среднекв. отклонение). Параметры рассчитаны для нашего ряда логарифмов. Конечная цена фьючерса для эмпирического распределения определяется по формуле
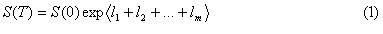
где li –логарифм Ln( S(i)/S (i-1)), случайно выбранный из нашего ряда.Для нормального распределения меняем li на ni
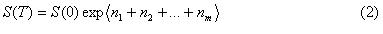
где ni – нормальная величина (0; ср.отклонение ряда li.)
Откуда же взялась улыбка там, где ее не должно быть?
Ответ в том, что, хотя нам казалось, что по построению мы исключили тренд, на самом деле положительный тренд возник. Ведь если цена непрерывно движется по броуновскому закону, как предполагается в модели БШ,

то c течением времени у логарифма цены возникает тренд

То есть, матожидание Ln(S(T)) – Ln(S(0)) равно (4). А у нас, напомню, эмпирическое распределение выбрано из ряда, в котором начальная и конечная цены совпадают, и, как следствие, матожидание Ln(S(T)) – Ln(S(0)) равно нулю . Таким образом, в нашем опыте с точки зрения модели БШ актив движется с положительным трендом µ, равным σ* σ /2 (T-t). Тренд повлиял на стоимость опционов колл, причем прирост стоимости опционов дальних страйков из-за тренда оказался не менее сильным (а по факту даже большим), чем для ближних. Искажение цен опционов привело к возникновению улыбки.
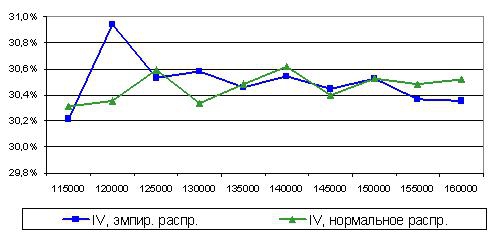
Замечу, что сам расчет цены опционов и их волатильности был некорректен. Если существует тренд, отличный от безрисковой ставки (которая для фьючерсов равна нулю), то инвестор не нейтрален к риску, ведь для риск-нейтрального инвестора все активы приносят один доход, равный безрисковой ставке. Если инвестор не риск-нейтрален, то считать стоимость опциона методом усреднения модельных терминальных цен нельзя, т.к. такой инвестор оценивает ценность прибыли и убытка по-разному. Внесем коррекцию, добавим тренд -σ* σ /2 (T-t) к эмпирическому и нормальному распределениям и нарисуем соответствующие улыбки

Мы видим, что отличия в улыбках минимальны. Они объясняются случайной ошибкой в рамках модели. Волатильность слева более чувствительна к ошибкам, поэтому размах колебаний выше. Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки на данном временном интервале. Замечу, что и в случае нескорректированной на тренд модели, отличия между двумя улыбками также минимальны и объясняются случайными ошибками.
Любопытно, что аналогичные выводы получаются, если использовать не эмпирическое, а другое распределение цен с толстыми хвостами, имеющее конечную дисперсию и матожидание. В частности, похожий опыт был когда-то поставлен мной для распределения Пирсона седьмого порядка с куртозисом, взятым из рыночного распределения. В этом случае улыбка также вырождается в прямую линию.
Причина отсутствия улыбки – Центральная Предельная Теорема, смысл которой состоит в том, что сумма независимых, одинаково распределенных случайных величин стремится в пределе к нормальному распределению. В нашем случае сумма величин li в формуле (1) дает величину, близкую к нормальной, в связи с большим периодом модели, равным ста шагам. Вопрос о меньшем количестве шагов модели будет рассмотрен в другой статье.
Эмпирическое распределение может быть построено и для приращений актива, которые не являются независимыми. В частности, в журнале ФиО n1-2 за 2009г. Израйлевичем и Цудикманом была представлена модель оценки опционов на основе доходности актива за периоды, равные времени до экспирации. Однако, применяя рассуждения, аналогичные изложенным выше, мы убедимся, что использование исторических рядов цен в общем случае приведет к возникновению тренда и искажению стоимости опционов в модели. Для более точной оценки модель должна быть скорректирована на тренд.
Выводы:
1. Эмпирическое распределение для оценки стоимости опционов следует применять с коррекцией на тренд.
2. В модели ежедневных независимых приращений цен актива, построенной на основе исторических данных, улыбки волатильности не возникает при сроках до экспирации выше 100 дней.
Ссылки
график ежедневных доходностей S&P 500 взят с сайта
http://managed-futures-blog.attaincapital.com/
теги блога broker25
- HV
- IV
- KZOS
- NKNC
- акции
- акции США
- алготрейдинг
- бабочка
- Брокер
- бэктестинг
- бюджет
- волатильность
- вор
- ВТБ
- второй эшелон
- газ
- газеты
- Газпром
- дельта-хеджирование
- дефицит бюджета
- дивиденды
- железный кондор
- здоровье трейдера
- зигзаг
- Индексы
- Историческая волатильность
- Казаньоргсинтез
- Китай
- корреляция активов
- макро
- ММВБ
- мультипликаторы
- Навальный
- накопительная часть пенсии
- налоги
- НДФЛ
- Нефть
- Нижнекамскнефтехим
- НПФ
- обмен акций
- опцион волатильность
- опционные спреды
- Опционы
- офф-топ
- оффтоп
- оценка акций
- поводыри
- приватизация
- прогноз
- прогноз по акциям
- продажа опционов
- продажа путов
- расчет в рублях
- реструктуризация
- рецензия на книгу
- Роснефть
- российский рынок акций
- Рынок акций США
- Саудовская Аравия
- Сибур
- сила Сибири
- Сила Сибири-2
- система
- скачать
- смартлаб конкурс
- сравнительный анализ
- суд
- сырье
- тест
- тики
- толстые хвосты
- Тольяттиазот
- торговые роботы
- улыбка
- улыбка волатильности
- философия трейдинга
- финанализ
- ФНБ
- фундаментальный анализ
- фундаметальный анализ
- хеджирование
- экспорт газа
- эмиссия денег
- Яндекс



















Я глубоко этим вопросом не занимался, но возможно стоит покопать в направлении оценок опционов под стохастической волатильностью или CEV-модели и т.д. Сейчас уже очень много понаридумывали альтернативных GBM процессов
Было бы интересно глянуть на аналогичные приведенным графики для 22 и 11 дней (месяц и полмесяца). 100 дней (4.5 месяца) — большой и довольно странный выбор срока. В первую очередь интересуют уже очищенные от тренда, так как иначе некорректно говорить об одной улыбке в принципе. Причем есть предложение рисовать улыбку в обе стороны от денег, поскольку форма в разные стороны разная.
Кстати, если вы нарисуете для 100 дней вправо тоже (но том же графике, что влево), то небольшой наклон, который угадывается глазами и сейчас (если выкинуть 2 крайних точки), может стать более заметным. Это к фразе: «Очевидно, что толстые хвосты нашего эмпирического распределения никак не повлияли на изгиб улыбки». Мне из того же графика видится, что повлияли, только несильно (а чего еще ждать от 4 с лишним месяцев?...)
То, что разбили на части — правильно. И читать целую «Войну и мир» никто не станет, и дискуссия в результате двух отдельных статьей выйдет плодотворнее и шире, чем после одного «трактата».
А вот ваши предварительные ощущения не мне кажутся верными, особенно для индексных опционов. Там где стоит жиденький маркет-мейкер и у кого-то появляются сильные желания сыграть направленно — там так может быть иногда (завышенные оценки опцоинов из-за заывашенных рисков). В Сбере и Газпроме, особенно одномесячном — запросто. А в индексе, на мой взгляд, маркет-мейкеров много, они довольно крепкие, так что там реально должна работать форма распределения + ожидания скачков волатильности (то есть, тоже негауссовосость мира, но в плане изменения волатильности). Если сумеете расчетами опровергнуть — будет интересно почитать.
О чем я говорил на 5-м НОКе 9 месяцев назад, уже не очень помню. Но скорее всего либо о статье Виталия Курбаковского в F&O, на которую у меня даже рабочей ссылки нет, поскольку к ней нельзя получить доступ по электронной подписке на сайте журнала. Я ниже написал Виталию, может, он где-нибудь обнародует формулы и их вывод еще раз.
Либо вот об этой статье:
users.ox.ac.uk/~ofrcinfo/file_links/mf_papers/2002mf04.pdf
Формулы цен опционов — (35) и (37) на стр. 26.
Каленкович, кстати, как-то упомянул, что он после разговора со мной полистал статью, понял, что потребуется очень много возиться, и решил идти своим путем. Так что не переоценивайте свои силы. Сами формулы — это еще страшно далеко от успешного трейдинга, и важно не зарыться с головой в математику и ее реализацию… Лучше взять что-то попроще, зато как следует «почувствовать» инструмент.
Касательно формул и трейдинга, я согласен. Мои торговые модели пока не имеют отношения к теории, но мне все это интересно для лучшего понимания процессов.
Касательно опровергнуть — идея есть, может руки дойдут. Но, в любом случае я не отказываюсь от теории
Есть два случайных процесса — f1,f2. Оба геометрические броуновские, но с разными волатильностями. Первый (f1) с низкой волатильностью (S1) – соответствует спокойному рынку
Второй (f2), с высокой волатильностью (S2) – быстрому рынку.
Есть вероятность Alfa.
Моделируем процесс – на каждом шаге с вероятностью Alf берем приращение из f1, с вероятностью (1-Alfa) – из f2.
У такого композитного процесса 3 параметра (S1,S2,Alfa). При их соответствующем подборе на выходе получится гистограмма приращений, очень похожая на эмпирическую. Скорее всего, S1 будет близок к “фоновому” значению VIX (10-12%). S2 – (80-90%).
Самый интересный параметр – Alfa – вероятность того, что рынок останется в спокойном состоянии. Именно он определяет ожидания игроков и, видимо, хорошо коррелирован с индексом волатильности VIX.
Для опционов с дальними сроками экспирации ничего нового мы не получим. Прогноз Alf даст не больше, чем прогноз VIX. А вот для ближних опционов, при nDays < 10, Alfa будет влиять еще и на форму кривой IV (в отличие от VIX).
Дальше можно так
– за 10 дней до экспирации подбираем параметр Alfa, чтобы расчетная кривая IV наилучшим образом совпала с рыночной- назовем его Alfa-Imp
— прогнозируем Alfa на 10 дней вперед (Alfa-Prog). Здесь нужно учитывать фундаментальные факторы. Например, если до конца недели ожидается заседание FOMC, вероятность остаться в “медленном” рынка становится близкой к 0. Если никаких событий не ожидается и общий фон спокойный – вероятнее всего, что и рынок останется спокойным – Alfa около 1. На срок до 10 дней такой прогноз вполне возможен.
— Рассчитываем теоретические цены опционов по Alfa-Prog – сравниваем с рыночными.
Наибольшая разница в ценах, вызванная неравенством Alfa-Imp и Alfa-Prog, должна достигаться именно на краях кривой волатильности, где в наибольшей степени заметны искажения, вызванные “тяжелыми” хвостами распределений
До аналитических формул такую модель ценообразования, скорее всего, раскрутить не удастся (вероятностная свертка распределений – жутко громоздкая штука), но посчитать теоретические цены численно совсем не сложно
Так что, возможно, на искажениях IV можно играть, но только на коротких сериях.
Потому, Даешь недельные опционы!
Виталий, с последним тезисом согласен, причем короткие опционы по моему разумению существенно нужнее тем, кто сейчас спекулирует фьючерсом, а не заядлым опционщикам.
Модель предлагаете в чем-то интересную, но, как верно замечаете, не считаемую… Да и почему режимов всего 2? Откуда брать эту непрерывно меняющуюся альфу? Короче, я бы сказал, что модель любопытная, но закапываться в нее не стоит…
А вот по поводу вашей модели улыбки (не с последнего НОКа) — которую вы когда-то публиковали в F&O. Вы не хотите ее еще раз опубликовать — ну, хоть на том же смарт-лабе? А то даже в разговоре отослать людей не к чему — доступ к архиву F&O за 2009-2010 год на сайте журнала не предлагается.
А ведь улыбка весьма интересная: параметров всего 3, один — волатильность на деньгах, еще 2 отвечают один за правое крыло, другой за левое. Вы сами-то пользуетесь той моделью или уже перешли к более современным разработкам?
Пробовал найти сайт ЗАО «Математика финансов» — думал, может, там статьи выкладываете, но не сумел. Шифруетесь или я искал плоховато?
Спасибо, что не отнеслись к модели серьезно — это первое, что пришло в голову, когда думал о том, можно ли играть на искажениях, вызванных тяжелыми хвостами. Очень хорошую идею подсказал broker25 (господи, насколько проще по имени обращаться) — играть можно, но только на коротких опционах и только тогда, когда будущее распределение явно отличается от прошлого, на основании которого сформировалось кривая IV.
Что касается статьи, спасибо за предложение. Здесь две проблемы. Первая — время, второе — не уверен, что она будет кому-то интересна. Подавляющее большинство опционных трейдеров вполне удовлетворены классической теорией. В этом смысле пост broker'a25 (господи, опять) очень показателен. Такое ощущение, что все остальные просто начитались Талеба и уверены, что «тяжелые хвосты» — это единственная причина искривления кривой IV. Здесь мне больше по душе предложение Каленковича — серьезные темы — для спецов.
С уважением, Курбаковский
PS Если не секрет, сами какие модели используете. Я — только свою, чего уж скромничать, она действительно хорошая.
сам пользуюсь подавленными устойчивыми Леви, ссылку на которую дал выше. Только пришлось еще «снаружи» к той модели добавить отрицательную корреляцию волы и базового актива — достаточно топорно и грубо, вне сути модели. Средней паршивости получился довесочек, но без его учета точно торговать нельзя.
Так что теперь уже, может, и не стал бы зарываться в Леви, раз все равно пришлось сверху навинчивать дополнительные сложности. Но, сейчас уж «привычка свыше нам дана» — как когда-то сделал, так и освоился уже, знаю, где что от каких параметров ждать. Это, кстати, очень важно при реальном трейдинге, что я уже отметил выше.
Сама модель устойчивых Леви тоже достаточно жесткая (классическая 3-х параметрическая, если делать дисперсию конечной, подавляя хвосты, как в статье по ссылке) — то 4-х. То есть, в этом плане близко к вашей по числу параметров.
broker25 выше мне ответил, что ваша статья опубликована в Вестнике Науфор. Я, кстати, не знал. Если они высылают — ну, наверное, тогда и нет смысла больше переопубликовывать.
Про сайт мне просто думалось, что он по логике позволяет привлекать клиентов — то есть, это вещь себя надежно окупающая (и при том весьма недорогая по сравнению с человеком-сейлзом :) ). Поэтому и удивился, что не нашел. Если надумаете опять поддерживать — надеюсь, разместите статьи. И сайт солиднее, и интересующимся опционной тематикой не надо никуда писать с просьбой им что-то выслать :).
Я торгую трендследящие стратегии с помошью роботов. Чисто эмпирически установил, что динамика волатильности — значимый фактор, учет которого очень полезен. Перебрал десятки примитивных способов расчета, от ATR до VIX, что-то реально использую. Хотелось бы понять Ваш подход. С уважением, Сергей.
С уважением, Курбаковский
С уважением, Сергей.
Второе — у Alfa есть физический смысл. Именно этим термином пользуются трейдеры при анализе рынка — грохнет или не грохнет до экспирации. Если может грохнуть, то с какой вероятностью, а это и есть Alfa. Для пары толковых студентов — отличная практика.
Я пока пытался разобраться с эмпирическим распределением.
У Вас же речь идет скорее о стохастической волатильности,
Думаю, на смартлабе есть народ, который этим занимался.
Может лучше идею повесить отдельным постом?
я мало занимался стох. волой, но конечно могу выразить свое имхо.
Стох. моделей много, но отличие Вашей в том, что она настраивается вручную.
Соответственно, бэктестить ее трудно.
Два варианта
1. Продавать после прыжка. Тогда калибровка по текущей улыбке и историческим изменениям улыбки после ожидаемых событий.
2. Держать до экспирации. Тогда возникает вопрос касательно адекватности улыбки на коротких сроках.
Возможно она выводится не только из свойств распределений. Есть еще страховая премия.
И премия за кредитные деньги ( из презентации).
И, конечно, моделей прыжков можно придумать много, даже с одним параметром Alfa
Тем не менее, Вам, broker25, она может оказаться полезной, объясняющей возникновение тяжелых хвостов и острой вершины эмпирического распределения. Будет время, помоделирую
У себя попробовал такую коррекцию: в историческом распределении приращений на каждое реальное приращение добавлял зеркальное, противоположного знака. У получившегося распределения цен на экспу МО стало равно текущему значению фьюча и пут-колл паритет стал выполняться идеально. Улыбка получилась с плоским горизонтальным дном. Это совпадает с Вашим вторым выводом. Правда у меня это получается на сроках и меньше 100дней. Вот улыбка, например, за два дня до экспы: www.novationz.ru/html/option_tester/pubimg/SmileIV_04.png. Края у нее подняты только потому, что ввел насильно условие: внутренняя стоимость опциона не может быть меньше 10п.
Если кол-во траекторий делать небольшим (1000, 10000), то дно получается кривое и только отдаленно напоминает горизонталь. Но при росте кол-ва, например, до 10млн траекторий, кривое дно вытягивается в идеальную горизонталь.
Не уверен правда, что допустимо делать такую коррекцию исторического распределения приращений (с добавлением зеркального приращения на каждое реальное). Наверное Ваша коррекция — более правильная. Правильно ли понимаю, что предлагаете из каждого реального приращения вычесть величину: (σ*σ/2)*(T-t)? И что такое (T-t)? Спасибо.
Видимо, я ошибочно вычитаю эту величину (σ*σ/2) из каждого приращения (ведь тренд может быть и вверх и вниз, а эта величина всегда положительная). Не подскажете, что именно нужно делать с (σ*σ/2)?
Насчет зеркальности, делал так: если допустим эмпирическое распределение приращений (считаю их как относительное изменение (S_i+1 — S_i)/S_i, а не через логарифм) состоит только из двух приращений, +0.01% и -0.02%, то для построения распределения цен на экспу добавляю зеркальные и использую такое распределение: (+0.01%, -0.02%, -0.01%, +0.02%). Получается симметричное распределение, без тренда. Но не уверен — допустима ли такая коррекция, не меняет ли это слишком сильно исходное эмпирическое распределение?
в конце беру экспоненту от суммы логарифмов,
чтобы избавиться от тренда, сначала вычесть среднее из каждого члена ряда логарифмов, а потом уже вычесть (σ*σ/2)
и все работает и теоретическое объяснение этому есть
— Минутки должны представлять репрезентативно и прыжки на следующий день и прыжки, которые получаются раз в один-два года. То есть испытаний должно быть очень много.
Длина торгового периода в минутах также весьма велика.
Я не знаю, хватит ли мощности ПК чтобы смоделировать этот процесс.
— я против зеркального отражения, тк форма эмпирического распределения слева и справа разная
С минутками и гепами поступаю так: создаю не одно, а три распределения приращений. Первое — приращения между минутками внутри дня, второе — приращения между последней минуткой вечерки и первой минуткой следующего дня, третье — приращения через выходные и праздники. И при генерации очередной траектории использую соответствующим образом все три распределения. Мне кажется, так будет вполне нормально учитывать гепы.
Строю распределение цен на экспу для каждого квартала отдельно. За квартал получается примерно 50тыс минуток. Если строить, например, 100000 траекторий длиной в три месяца, то у меня на ноуте примерно 5 минут занимают вычисления.
Насчет несимметричности распределения приращений. Смотрел все кварталы с 2010 (фьюч RTS). На глаз все распределения были вроде симметричны. Да и в БШ предполагают что распределение приращений — нормальное, а значит симметричное. Вот и решил попробовать внести насильно симметрию в эмпирическое распределение. Все равно, по идее, это должно более точное распределение цен на экспу дать, чем то что по БШ получается.
если хотите репрезентативное распределение на экспирацию, то надо включать данные за несколько лет. И траекторий столько, чтобы хотя бы 100 раз случались крупные гэпы. У меня если больше миллиона траекторий, то точнее результаты.
Распределение несимметрично, это хорошо видно если посчитать площадь хвоста слева и справа
Думаю, может нужно полученное распределение цен на экспу (сгенерированное на приращениях) дополнительно подкорректировать (как-нибудь увеличить хвосты) так, чтобы при вычислении стоимости опционов на дальних страйках сразу выполнялось условие: внутренняя стоимость не меньше 10п. Может тогда моя ломанная улыбка превратиться в плавно изогнутую? Или плавная парабола должна получаться и без таких коррекций?